Joint Learning of Graph Representation and Node Features in Graph Convolutional Neural Networks
Paper and Code
Sep 11, 2019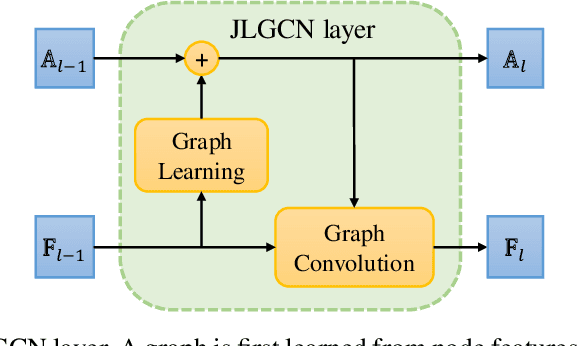
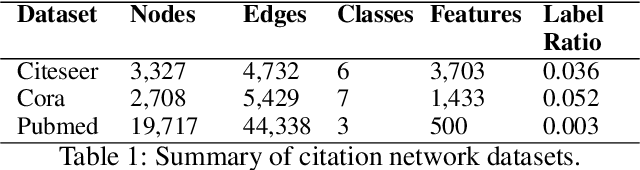
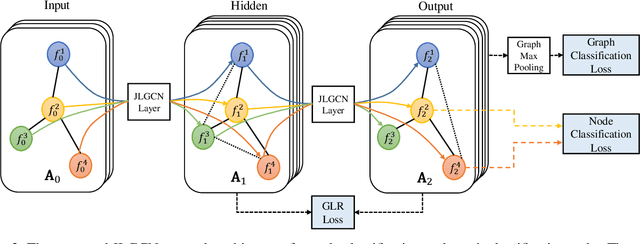
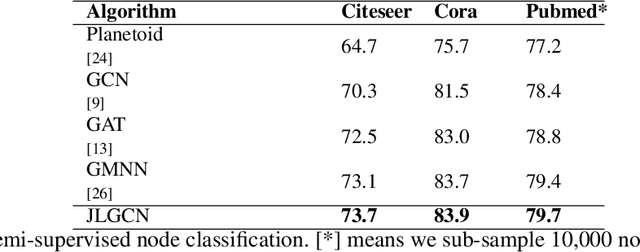
Graph Convolutional Neural Networks (GCNNs) extend classical CNNs to graph data domain, such as brain networks, social networks and 3D point clouds. It is critical to identify an appropriate graph for the subsequent graph convolution. Existing methods manually construct or learn one fixed graph for all the layers of a GCNN. In order to adapt to the underlying structure of node features in different layers, we propose dynamic learning of graphs and node features jointly in GCNNs. In particular, we cast the graph optimization problem as distance metric learning to capture pairwise similarities of features in each layer. We deploy the Mahalanobis distance metric and further decompose the metric matrix into a low-dimensional matrix, which converts graph learning to the optimization of a low-dimensional matrix for efficient implementation. Extensive experiments on point clouds and citation network datasets demonstrate the superiority of the proposed method in terms of both accuracies and robustness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge