JAWS: Predictive Inference Under Covariate Shift
Paper and Code
Jul 21, 2022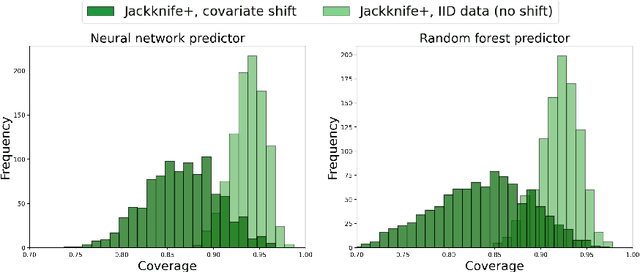
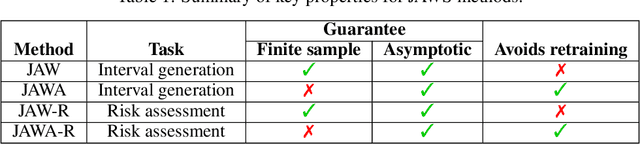
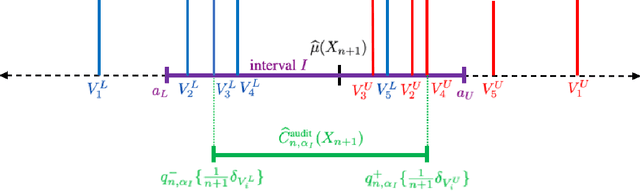
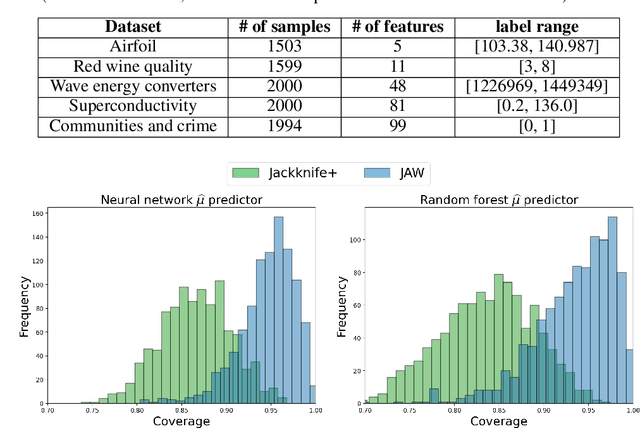
We propose \textbf{JAWS}, a series of wrapper methods for distribution-free uncertainty quantification tasks under covariate shift, centered on our core method \textbf{JAW}, the \textbf{JA}ckknife+ \textbf{W}eighted with likelihood-ratio weights. JAWS also includes computationally efficient \textbf{A}pproximations of JAW using higher-order influence functions: \textbf{JAWA}. Theoretically, we show that JAW relaxes the jackknife+'s assumption of data exchangeability to achieve the same finite-sample coverage guarantee even under covariate shift. JAWA further approaches the JAW guarantee in the limit of either the sample size or the influence function order under mild assumptions. Moreover, we propose a general approach to repurposing any distribution-free uncertainty quantification method and its guarantees to the task of risk assessment: a task that generates the estimated probability that the true label lies within a user-specified interval. We then propose \textbf{JAW-R} and \textbf{JAWA-R} as the repurposed versions of proposed methods for \textbf{R}isk assessment. Practically, JAWS outperform the state-of-the-art predictive inference baselines in a variety of biased real world data sets for both interval-generation and risk-assessment auditing tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge