Jacobian Methods for Dynamic Polarization Control in Optical Applications
Paper and Code
Aug 29, 2022
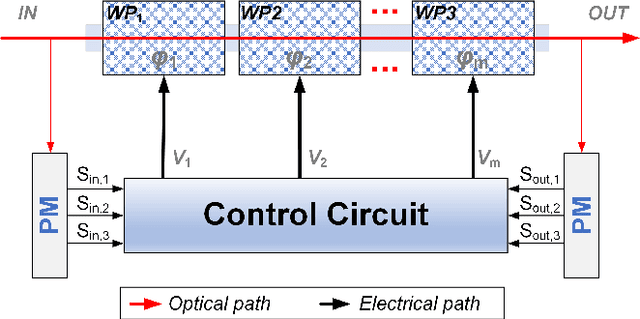
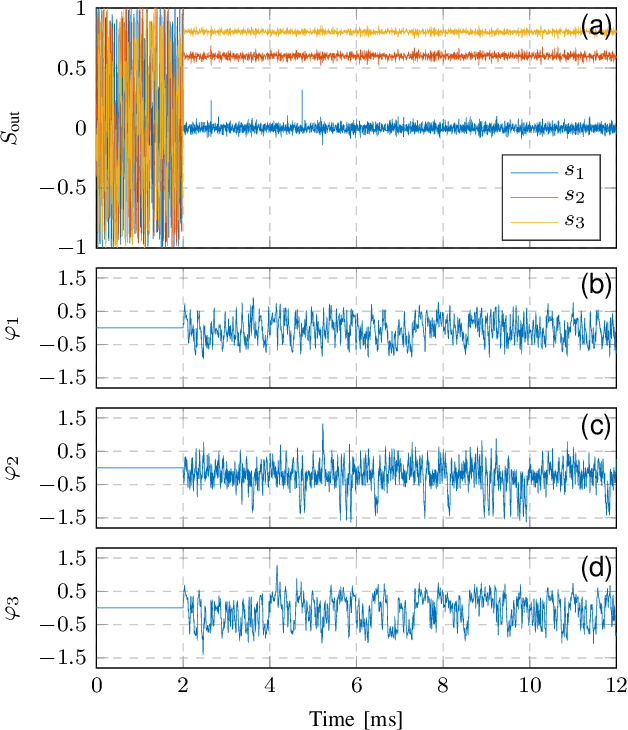
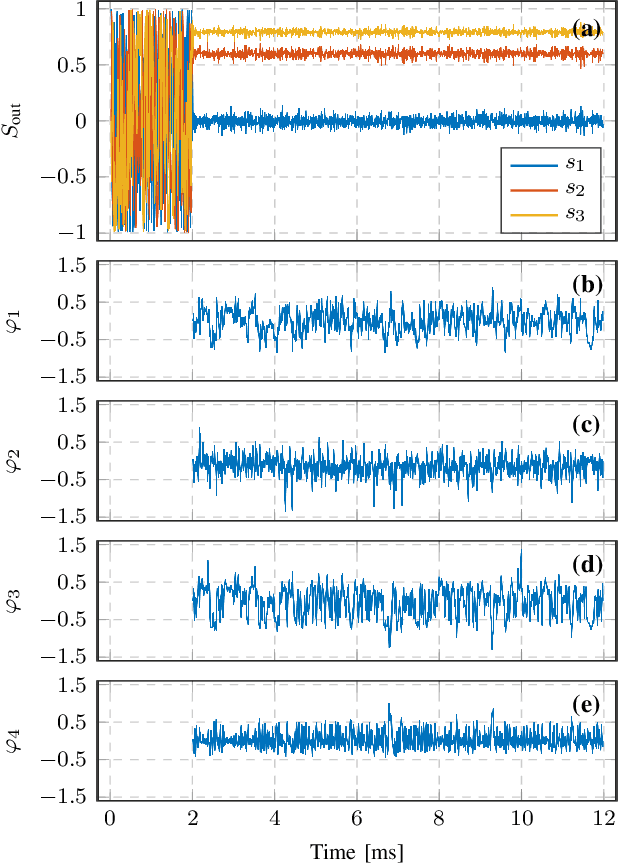
Dynamic polarization control (DPC) is beneficial for many optical applications. It uses adjustable waveplates to perform automatic polarization tracking and manipulation. Efficient algorithms are essential to realizing an endless polarization control process at high speed. However, the standard gradientbased algorithm is not well analyzed. Here we model the DPC with a Jacobian-based control theory framework that finds a lot in common with robot kinematics. We then give a detailed analysis of the condition of the Stokes vector gradient as a Jacobian matrix. We identify the multi-stage DPC as a redundant system enabling control algorithms with null-space operations. An efficient, reset-free algorithm can be found. We anticipate more customized DPC algorithms to follow the same framework in various optical systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge