Iterative Channel Estimation for Discrete Denoising under Channel Uncertainty
Paper and Code
Feb 24, 2019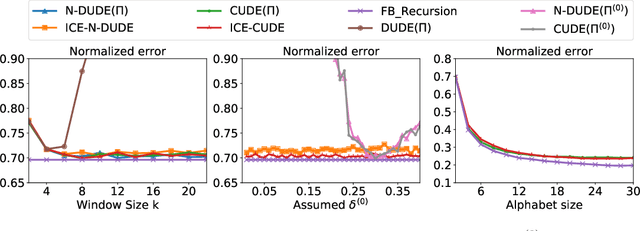
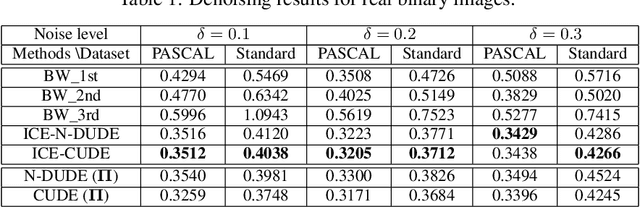
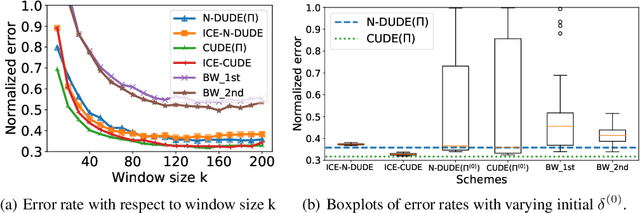
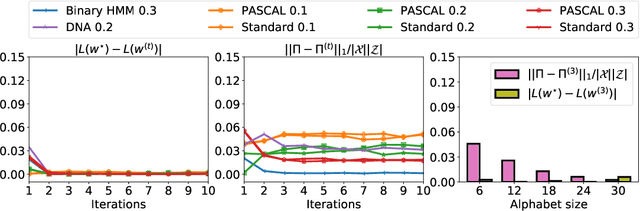
We propose a novel iterative channel estimation (ICE) algorithm that essentially removes the critical known noisy channel assumption for universal discrete denoising problem. Our algorithm is based on Neural DUDE (N-DUDE), a recently proposed neural network-based discrete denoiser, and it estimates the channel transition matrix as well as the neural network parameters in an alternating manner until convergence. While we do not make any probabilistic assumption on the underlying clean data, our ICE resembles Expectation-Maximization (EM) with variational approximation, and it takes advantage of the property of N-DUDE being locally robust around the true channel. With extensive experiments on several radically different types of data, we show that the ICE equipped N-DUDE (dubbed as ICE-N-DUDE) can perform \emph{universally} well regardless of the uncertainties in both the channel and the clean source. Moreover, we show ICE-N-DUDE becomes extremely robust to its hyperparameters and significantly outperforms the strong baseline that can deal with the channel uncertainties for denoising, the widely used Baum-Welch (BW) algorithm for hidden Markov models (HMM).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge