Iterated Filters for Nonlinear Transition Models

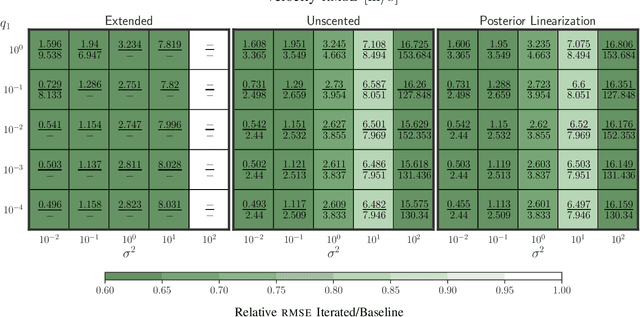
A new class of iterated linearization-based nonlinear filters, dubbed dynamically iterated filters, is presented. Contrary to regular iterated filters such as the iterated extended Kalman filter (IEKF), iterated unscented Kalman filter (IUKF) and iterated posterior linearization filter (IPLF), dynamically iterated filters also take nonlinearities in the transition model into account. The general filtering algorithm is shown to essentially be a (locally over one time step) iterated Rauch-Tung-Striebel smoother. Three distinct versions of the dynamically iterated filters are especially investigated: analogues to the IEKF, IUKF and IPLF. The developed algorithms are evaluated on 25 different noise configurations of a tracking problem with a nonlinear transition model and linear measurement model, a scenario where conventional iterated filters are not useful. Even in this "simple" scenario, the dynamically iterated filters are shown to have superior root mean-squared error performance as compared to their respective baselines, the EKF and UKF. Particularly, even though the EKF diverges in 22 out of 25 configurations, the dynamically iterated EKF remains stable in 20 out of 25 scenarios, only diverging under high noise.