It's Hard for Neural Networks To Learn the Game of Life

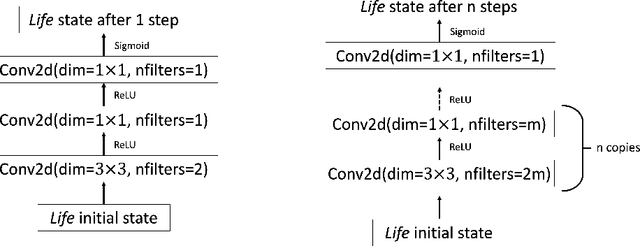
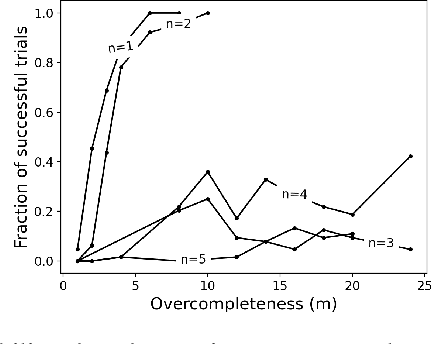
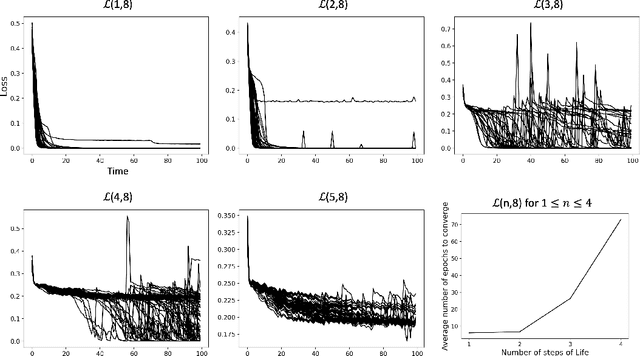
Efforts to improve the learning abilities of neural networks have focused mostly on the role of optimization methods rather than on weight initializations. Recent findings, however, suggest that neural networks rely on lucky random initial weights of subnetworks called "lottery tickets" that converge quickly to a solution. To investigate how weight initializations affect performance, we examine small convolutional networks that are trained to predict n steps of the two-dimensional cellular automaton Conway's Game of Life, the update rules of which can be implemented efficiently in a 2n+1 layer convolutional network. We find that networks of this architecture trained on this task rarely converge. Rather, networks require substantially more parameters to consistently converge. In addition, near-minimal architectures are sensitive to tiny changes in parameters: changing the sign of a single weight can cause the network to fail to learn. Finally, we observe a critical value d_0 such that training minimal networks with examples in which cells are alive with probability d_0 dramatically increases the chance of convergence to a solution. We conclude that training convolutional neural networks to learn the input/output function represented by n steps of Game of Life exhibits many characteristics predicted by the lottery ticket hypothesis, namely, that the size of the networks required to learn this function are often significantly larger than the minimal network required to implement the function.