Isotonic Data Augmentation for Knowledge Distillation
Paper and Code
Jul 06, 2021

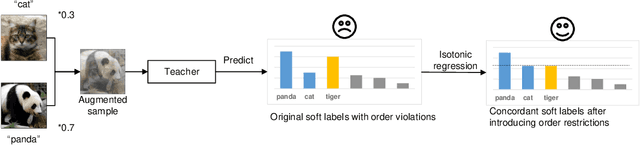

Knowledge distillation uses both real hard labels and soft labels predicted by teacher models as supervision. Intuitively, we expect the soft labels and hard labels to be concordant w.r.t. their orders of probabilities. However, we found critical order violations between hard labels and soft labels in augmented samples. For example, for an augmented sample $x=0.7*panda+0.3*cat$, we expect the order of meaningful soft labels to be $P_\text{soft}(panda|x)>P_\text{soft}(cat|x)>P_\text{soft}(other|x)$. But real soft labels usually violate the order, e.g. $P_\text{soft}(tiger|x)>P_\text{soft}(panda|x)>P_\text{soft}(cat|x)$. We attribute this to the unsatisfactory generalization ability of the teacher, which leads to the prediction error of augmented samples. Empirically, we found the violations are common and injure the knowledge transfer. In this paper, we introduce order restrictions to data augmentation for knowledge distillation, which is denoted as isotonic data augmentation (IDA). We use isotonic regression (IR) -- a classic technique from statistics -- to eliminate the order violations. We show that IDA can be modeled as a tree-structured IR problem. We thereby adapt the classical IRT-BIN algorithm for optimal solutions with $O(c \log c)$ time complexity, where $c$ is the number of labels. In order to further reduce the time complexity, we also propose a GPU-friendly approximation with linear time complexity. We have verified on variant datasets and data augmentation techniques that our proposed IDA algorithms effectively increases the accuracy of knowledge distillation by eliminating the rank violations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge