Is Ordered Weighted $\ell_1$ Regularized Regression Robust to Adversarial Perturbation? A Case Study on OSCAR
Paper and Code
Oct 03, 2018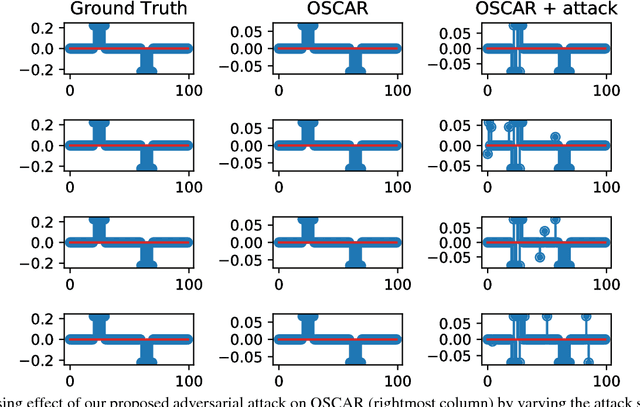
Many state-of-the-art machine learning models such as deep neural networks have recently shown to be vulnerable to adversarial perturbations, especially in classification tasks. Motivated by adversarial machine learning, in this paper we investigate the robustness of sparse regression models with strongly correlated covariates to adversarially designed measurement noises. Specifically, we consider the family of ordered weighted $\ell_1$ (OWL) regularized regression methods and study the case of OSCAR (octagonal shrinkage clustering algorithm for regression) in the adversarial setting. Under a norm-bounded threat model, we formulate the process of finding a maximally disruptive noise for OWL-regularized regression as an optimization problem and illustrate the steps towards finding such a noise in the case of OSCAR. Experimental results demonstrate that the regression performance of grouping strongly correlated features can be severely degraded under our adversarial setting, even when the noise budget is significantly smaller than the ground-truth signals.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge