Is an encoder within reach?

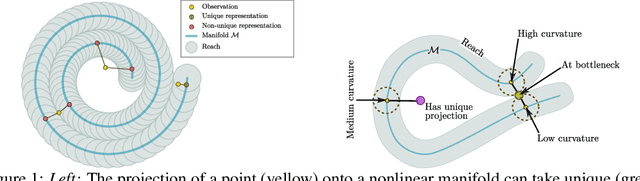
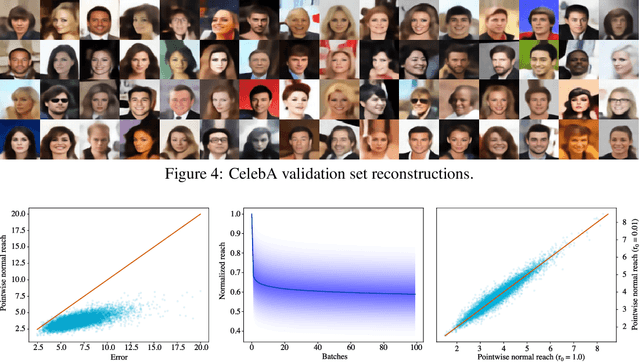
The encoder network of an autoencoder is an approximation of the nearest point projection onto the manifold spanned by the decoder. A concern with this approximation is that, while the output of the encoder is always unique, the projection can possibly have infinitely many values. This implies that the latent representations learned by the autoencoder can be misleading. Borrowing from geometric measure theory, we introduce the idea of using the reach of the manifold spanned by the decoder to determine if an optimal encoder exists for a given dataset and decoder. We develop a local generalization of this reach and propose a numerical estimator thereof. We demonstrate that this allows us to determine which observations can be expected to have a unique, and thereby trustworthy, latent representation. As our local reach estimator is differentiable, we investigate its usage as a regularizer and show that this leads to learned manifolds for which projections are more often unique than without regularization.