Investigation of large-scale extended Granger causality (lsXGC) on synthetic functional MRI data
Paper and Code
May 06, 2022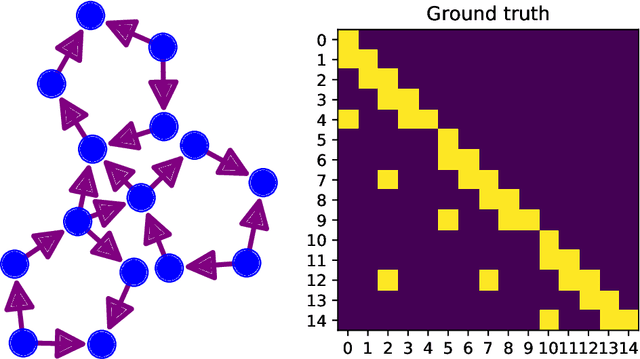
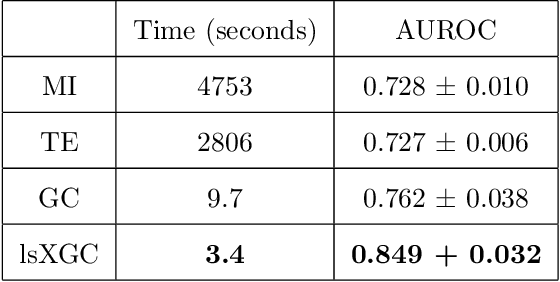
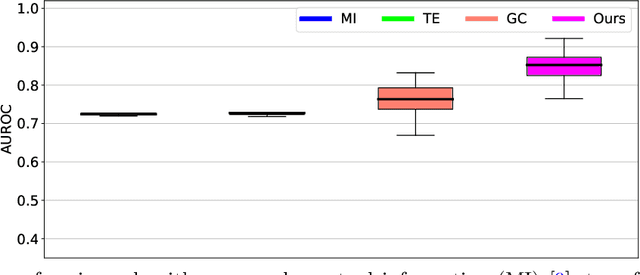
It is a challenging research endeavor to infer causal relationships in multivariate observational time-series. Such data may be represented by graphs, where nodes represent time-series, and edges directed causal influence scores between them. If the number of nodes exceeds the number of temporal observations, conventional methods, such as standard Granger causality, are of limited value, because estimating free parameters of time-series predictors lead to underdetermined problems. A typical example for this situation is functional Magnetic Resonance Imaging (fMRI), where the number of nodal observations is large, usually ranging from $10^2$ to $10^5$ time-series, while the number of temporal observations is low, usually less than $10^3$. Hence, innovative approaches are required to address the challenges arising from such data sets. Recently, we have proposed the large-scale Extended Granger Causality (lsXGC) algorithm, which is based on augmenting a dimensionality-reduced representation of the system's state-space by supplementing data from the conditional source time-series taken from the original input space. Here, we apply lsXGC on synthetic fMRI data with known ground truth and compare its performance to state-of-the-art methods by leveraging the benefits of information-theoretic approaches. Our results suggest that the proposed lsXGC method significantly outperforms existing methods, both in diagnostic accuracy with Area Under the Receiver Operating Characteristic (AUROC = $0.849$ vs.~$[0.727, 0.762]$ for competing methods, $p<\!10^{-8}$), and computation time ($3.4$ sec vs.~[$9.7$, $4.8 \times 10^3$] sec for competing methods) benchmarks, demonstrating the potential of lsXGC for analyzing large-scale networks in neuroimaging studies of the human brain.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge