Invertible Gaussian Reparameterization: Revisiting the Gumbel-Softmax

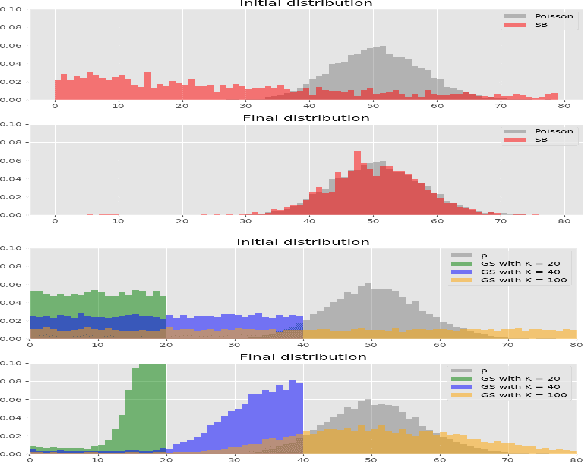
The Gumbel-Softmax is a continuous distribution over the simplex that is often used as a relaxation of discrete distributions. Because it can be readily interpreted and easily reparameterized, it enjoys widespread use. Unfortunately, we show that the cost of this aesthetic interpretability is material: the temperature hyperparameter must be set too high, KL estimates are noisy, and as a result, performance suffers. We circumvent the previous issues by proposing a much simpler and more flexible reparameterizable family of distributions that transforms Gaussian noise into a one-hot approximation through an invertible function. This invertible function is composed of a modified softmax and can incorporate diverse transformations that serve different specific purposes. For example, the stick-breaking procedure allows us to extend the reparameterization trick to distributions with countably infinite support, or normalizing flows let us increase the flexibility of the distribution. Our construction improves numerical stability and outperforms the Gumbel-Softmax in a variety of experiments while generating samples that are closer to their discrete counterparts and achieving lower-variance gradients.