Inverse Reinforcement Learning with Gaussian Process
Paper and Code
Jan 21, 2013

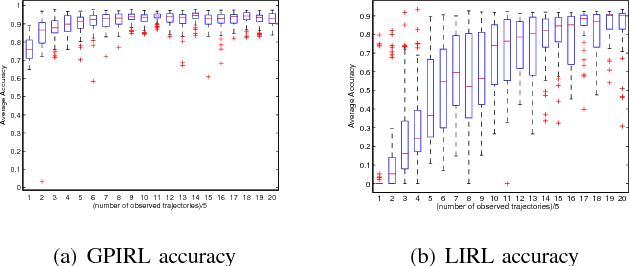

We present new algorithms for inverse reinforcement learning (IRL, or inverse optimal control) in convex optimization settings. We argue that finite-space IRL can be posed as a convex quadratic program under a Bayesian inference framework with the objective of maximum a posterior estimation. To deal with problems in large or even infinite state space, we propose a Gaussian process model and use preference graphs to represent observations of decision trajectories. Our method is distinguished from other approaches to IRL in that it makes no assumptions about the form of the reward function and yet it retains the promise of computationally manageable implementations for potential real-world applications. In comparison with an establish algorithm on small-scale numerical problems, our method demonstrated better accuracy in apprenticeship learning and a more robust dependence on the number of observations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge