Inverse Reinforcement Learning for Sequential Hypothesis Testing and Search

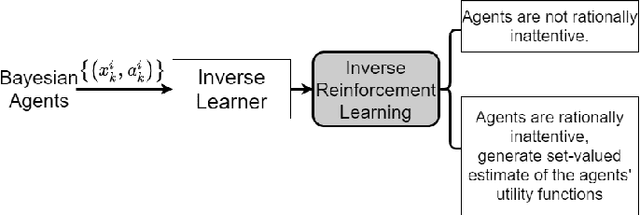
This paper considers a novel formulation of inverse reinforcement learning~(IRL) with behavioral economics constraints to address inverse sequential hypothesis testing (SHT) and inverse search in Bayesian agents. We first estimate the stopping and search costs by observing the actions of these agents using Bayesian revealed preference from microeconomics and rational inattention from behavioral economics. We also solve the inverse problem of the more general rationally inattentive SHT where the agent incorporates controlled sensing by optimally choosing from various sensing modes. Second, we design statistical hypothesis tests with bounded Type-I and Type-II error probabilities to detect if the agents are Bayesian utility maximizers when their actions are measured in noise. By dynamically tuning the prior specified to the agents, we formulate an {\em active} IRL framework which enhances these detection tests and minimizes their Type-II and Type-I error probabilities of utility maximization detection. Finally, we give a finite sample complexity result which provides finite sample bounds on the error probabilities of the detection tests.