Inverse Learning of Symmetry Transformations

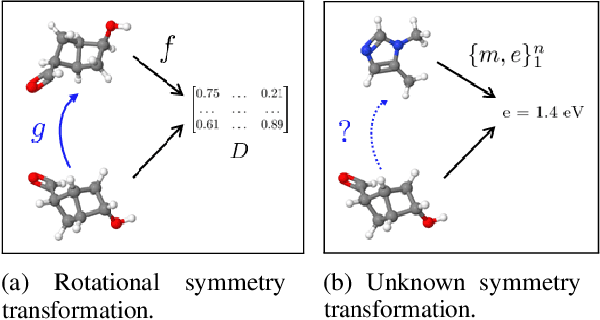
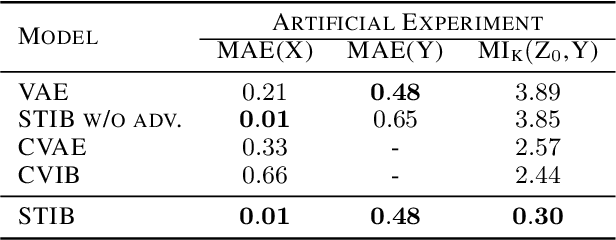
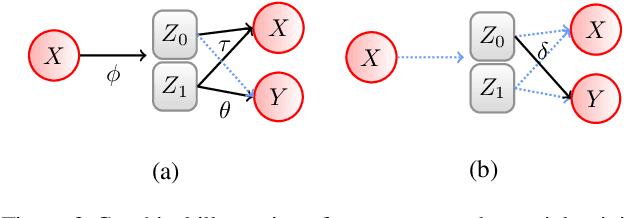
Symmetry transformations induce invariances and are a crucial building block of modern machine learning algorithms. Some transformations can be described analytically, e.g. geometric invariances. However, in many complex domains, such as the chemical space, invariances can be observed yet the corresponding symmetry transformation cannot be formulated analytically. Thus, the goal of our work is to learn the symmetry transformation that induced this invariance. To address this task, we propose learning two latent subspaces, where the first subspace captures the property and the second subspace the remaining invariant information. Our approach is based on the deep information bottleneck principle in combination with a mutual information regulariser. Unlike previous methods however, we focus on estimating mutual information in continuous rather than binary settings. This poses many challenges as mutual information cannot be meaningfully minimised in continuous domains. Therefore, we base the calculation of mutual information on correlation matrices in combination with a bijective variable transformation. Extensive experiments demonstrate that our model outperforms state-of-the-art methods on artificial and molecular datasets.