Interventional Causal Representation Learning

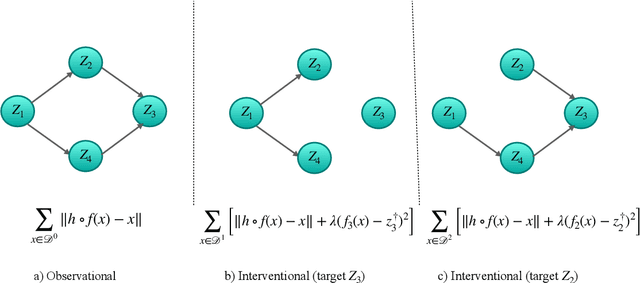
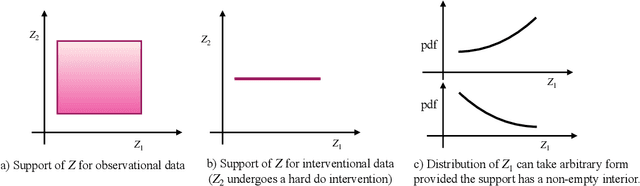
The theory of identifiable representation learning aims to build general-purpose methods that extract high-level latent (causal) factors from low-level sensory data. Most existing works focus on identifiable representation learning with observational data, relying on distributional assumptions on latent (causal) factors. However, in practice, we often also have access to interventional data for representation learning. How can we leverage interventional data to help identify high-level latents? To this end, we explore the role of interventional data for identifiable representation learning in this work. We study the identifiability of latent causal factors with and without interventional data, under minimal distributional assumptions on the latents. We prove that, if the true latent variables map to the observed high-dimensional data via a polynomial function, then representation learning via minimizing the standard reconstruction loss of autoencoders identifies the true latents up to affine transformation. If we further have access to interventional data generated by hard $do$ interventions on some of the latents, then we can identify these intervened latents up to permutation, shift and scaling.