Intersectional Fairness: A Fractal Approach

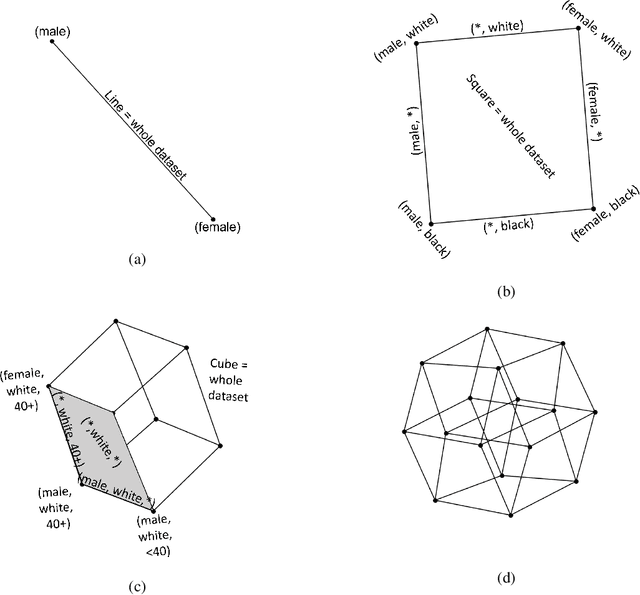
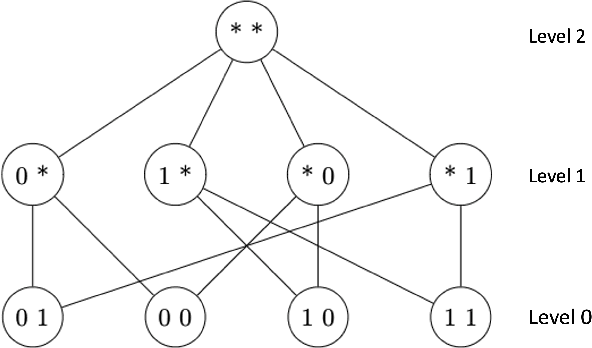
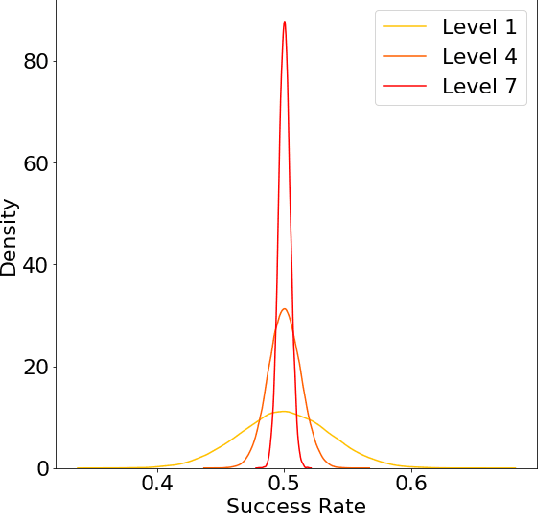
The issue of fairness in AI has received an increasing amount of attention in recent years. The problem can be approached by looking at different protected attributes (e.g., ethnicity, gender, etc) independently, but fairness for individual protected attributes does not imply intersectional fairness. In this work, we frame the problem of intersectional fairness within a geometrical setting. We project our data onto a hypercube, and split the analysis of fairness by levels, where each level encodes the number of protected attributes we are intersecting over. We prove mathematically that, while fairness does not propagate "down" the levels, it does propagate "up" the levels. This means that ensuring fairness for all subgroups at the lowest intersectional level (e.g., black women, white women, black men and white men), will necessarily result in fairness for all the above levels, including each of the protected attributes (e.g., ethnicity and gender) taken independently. We also derive a formula describing the variance of the set of estimated success rates on each level, under the assumption of perfect fairness. Using this theoretical finding as a benchmark, we define a family of metrics which capture overall intersectional bias. Finally, we propose that fairness can be metaphorically thought of as a "fractal" problem. In fractals, patterns at the smallest scale repeat at a larger scale. We see from this example that tackling the problem at the lowest possible level, in a bottom-up manner, leads to the natural emergence of fair AI. We suggest that trustworthiness is necessarily an emergent, fractal and relational property of the AI system.