Intersection of Parallels as an Early Stopping Criterion
Paper and Code
Aug 19, 2022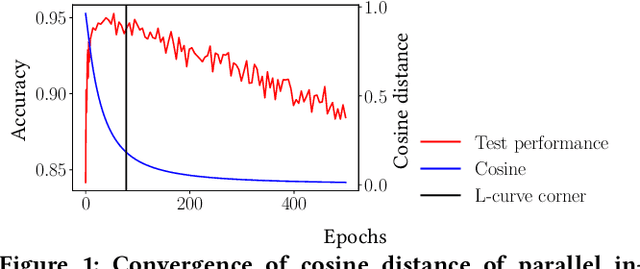
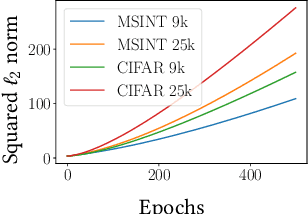
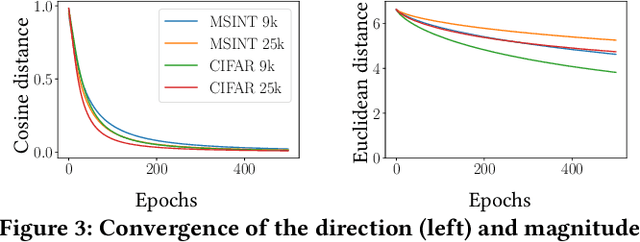
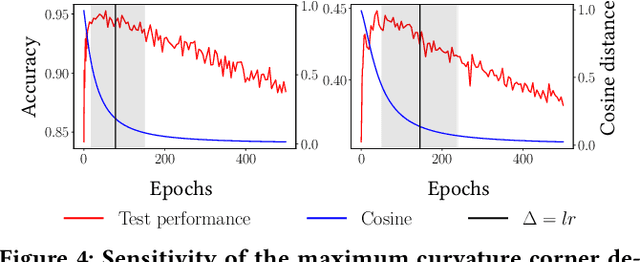
A common way to avoid overfitting in supervised learning is early stopping, where a held-out set is used for iterative evaluation during training to find a sweet spot in the number of training steps that gives maximum generalization. However, such a method requires a disjoint validation set, thus part of the labeled data from the training set is usually left out for this purpose, which is not ideal when training data is scarce. Furthermore, when the training labels are noisy, the performance of the model over a validation set may not be an accurate proxy for generalization. In this paper, we propose a method to spot an early stopping point in the training iterations without the need for a validation set. We first show that in the overparameterized regime the randomly initialized weights of a linear model converge to the same direction during training. Using this result, we propose to train two parallel instances of a linear model, initialized with different random seeds, and use their intersection as a signal to detect overfitting. In order to detect intersection, we use the cosine distance between the weights of the parallel models during training iterations. Noticing that the final layer of a NN is a linear map of pre-last layer activations to output logits, we build on our criterion for linear models and propose an extension to multi-layer networks, using the new notion of counterfactual weights. We conduct experiments on two areas that early stopping has noticeable impact on preventing overfitting of a NN: (i) learning from noisy labels; and (ii) learning to rank in IR. Our experiments on four widely used datasets confirm the effectiveness of our method for generalization. For a wide range of learning rates, our method, called Cosine-Distance Criterion (CDC), leads to better generalization on average than all the methods that we compare against in almost all of the tested cases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge