Interpolating Compressed Parameter Subspaces

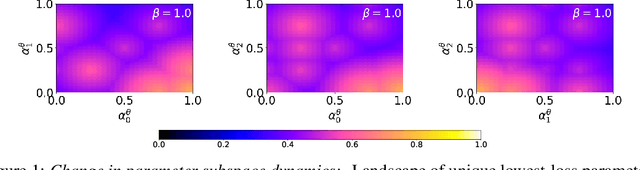
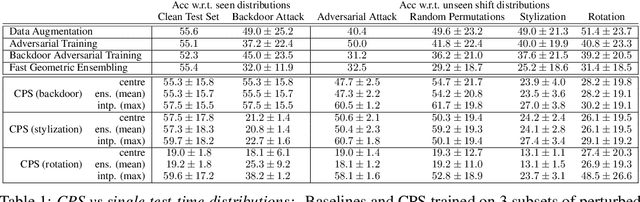
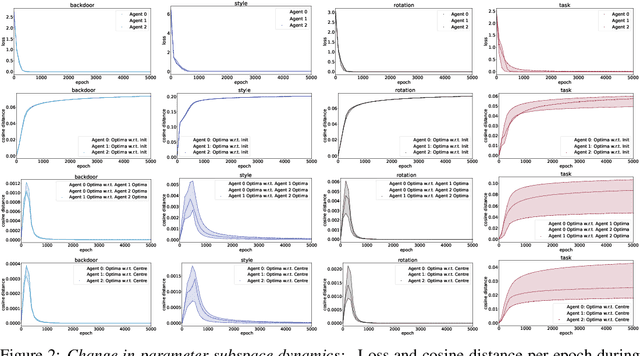
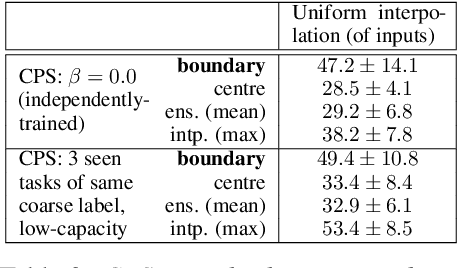
Inspired by recent work on neural subspaces and mode connectivity, we revisit parameter subspace sampling for shifted and/or interpolatable input distributions (instead of a single, unshifted distribution). We enforce a compressed geometric structure upon a set of trained parameters mapped to a set of train-time distributions, denoting the resulting subspaces as Compressed Parameter Subspaces (CPS). We show the success and failure modes of the types of shifted distributions whose optimal parameters reside in the CPS. We find that ensembling point-estimates within a CPS can yield a high average accuracy across a range of test-time distributions, including backdoor, adversarial, permutation, stylization and rotation perturbations. We also find that the CPS can contain low-loss point-estimates for various task shifts (albeit interpolated, perturbed, unseen or non-identical coarse labels). We further demonstrate this property in a continual learning setting with CIFAR100.