Information-Theoretic Generalization Bounds for Transductive Learning and its Applications

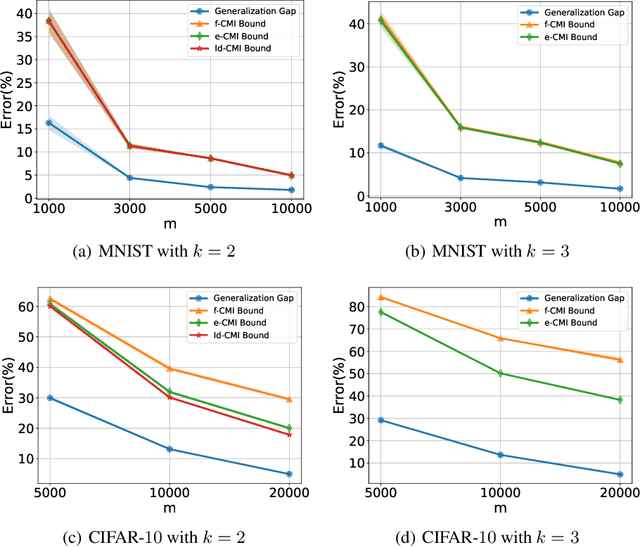
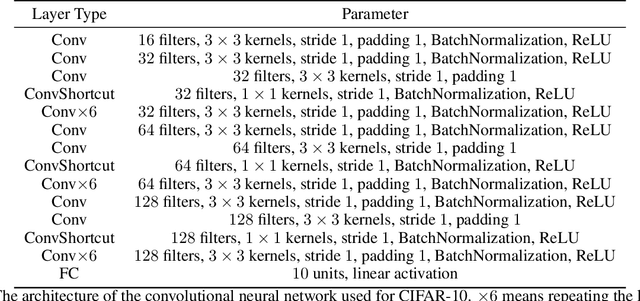
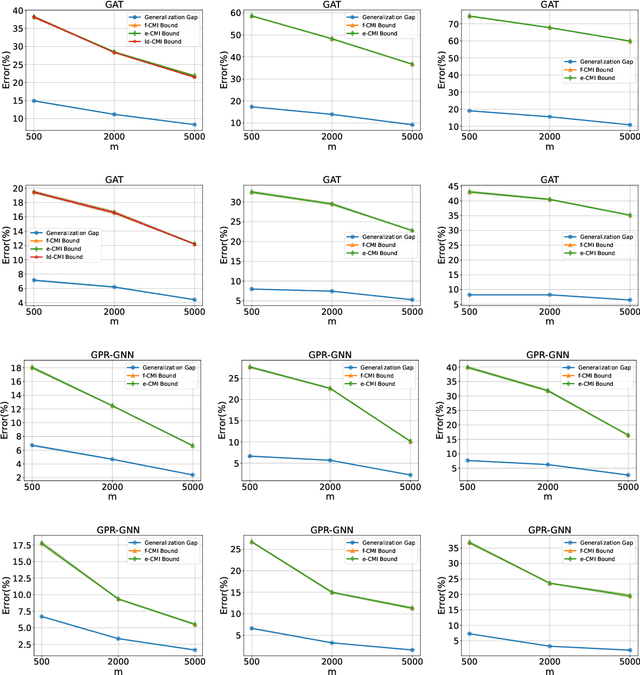
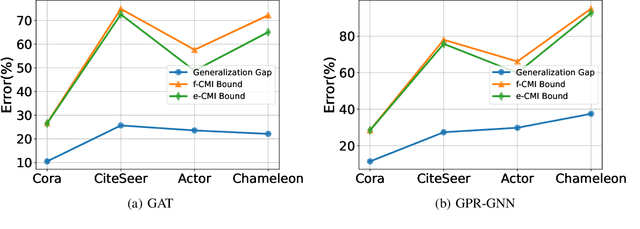
In this paper, we develop data-dependent and algorithm-dependent generalization bounds for transductive learning algorithms in the context of information theory for the first time. We show that the generalization gap of transductive learning algorithms can be bounded by the mutual information between training labels and hypothesis. By innovatively proposing the concept of transductive supersamples, we go beyond the inductive learning setting and establish upper bounds in terms of various information measures. Furthermore, we derive novel PAC-Bayesian bounds and build the connection between generalization and loss landscape flatness under the transductive learning setting. Finally, we present the upper bounds for adaptive optimization algorithms and demonstrate the applications of results on semi-supervised learning and graph learning scenarios. Our theoretic results are validated on both synthetic and real-world datasets.