Information Perspective to Probabilistic Modeling: Boltzmann Machines versus Born Machines
Paper and Code
Dec 12, 2017
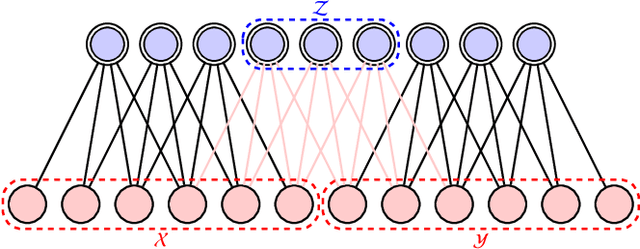
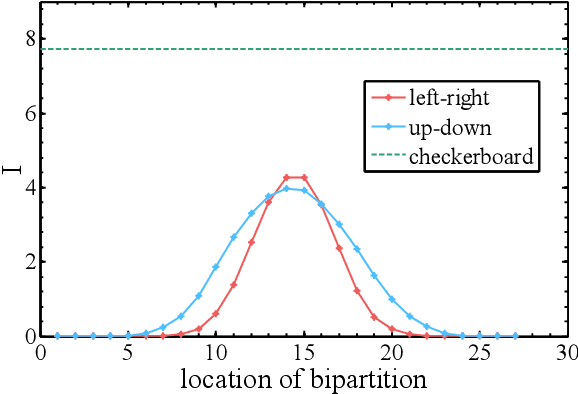
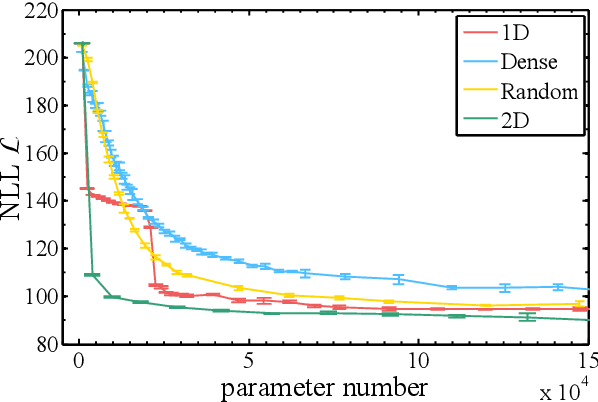
We compare and contrast the statistical physics and quantum physics inspired approaches for unsupervised generative modeling of classical data. The two approaches represent probabilities of observed data using energy-based models and quantum states respectively.Classical and quantum information patterns of the target datasets therefore provide principled guidelines for structural design and learning in these two approaches. Taking the restricted Boltzmann machines (RBM) as an example, we analyze the information theoretical bounds of the two approaches. We verify our reasonings by comparing the performance of RBMs of various architectures on the standard MNIST datasets.
* Entropy 2018, 20(8), 583 * 7 pages, 4 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge