Information Assisted Dictionary Learning for fMRI data analysis

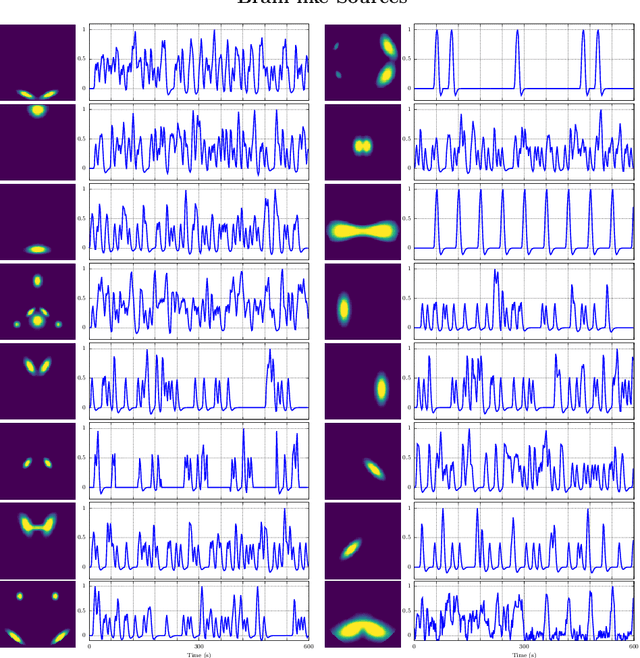
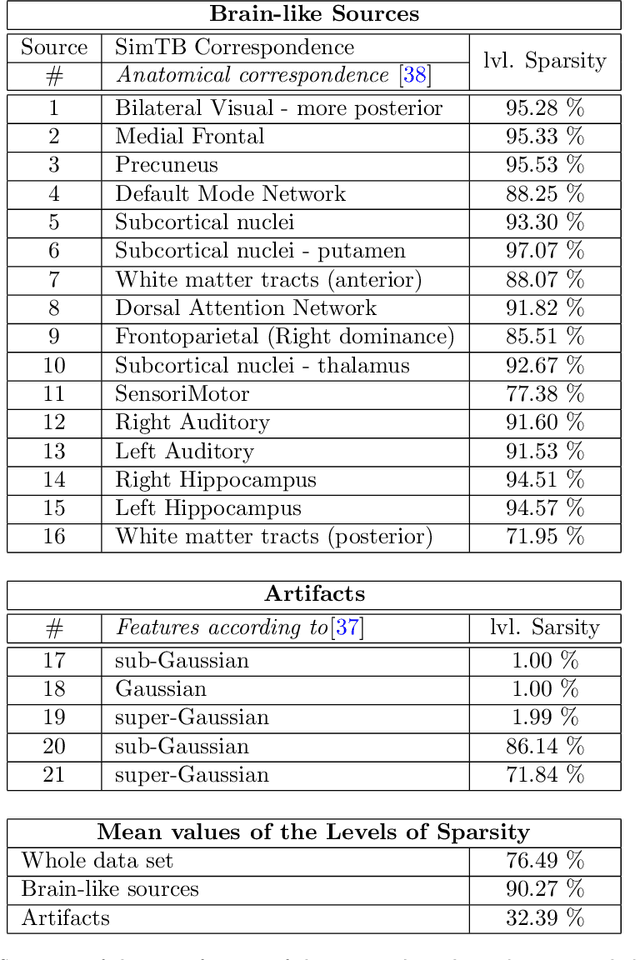
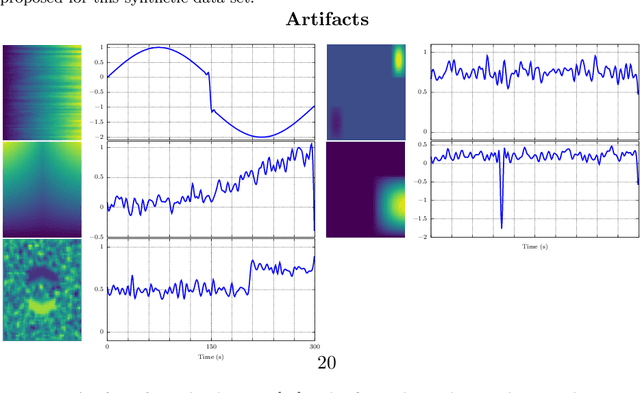
In this paper, the task-related fMRI problem is treated in its matrix factorization formulation. The focus of the reported work is on the dictionary learning (DL) matrix factorization approach. A major novelty of the paper lies in the incorporation of well-established assumptions associated with the GLM technique, which is currently in use by the neuroscientists. These assumptions are embedded as constraints in the DL formulation. In this way, our approach provides a framework of combining well-established and understood techniques with a more ``modern'' and powerful tool. Furthermore, this paper offers a way to relax a major drawback associated with DL techniques; that is, the proper tuning of the DL regularization parameter. This parameter plays a critical role in DL-based fMRI analysis since it essentially determines the shape and structures of the estimated functional brain networks. However, in actual fMRI data analysis, the lack of ground truth renders the a priori choice of the regularization parameter a truly challenging task. Indeed, the values of the DL regularization parameter, associated with the $\ell_1$ sparsity promoting norm, do not convey any tangible physical meaning. So it is practically difficult to guess its proper value. In this paper, the DL problem is reformulated around a sparsity-promoting constraint that can directly be related to the minimum amount of voxels that the spatial maps of the functional brain networks occupy. Such information is documented and it is readily available to neuroscientists and experts in the field. The proposed method is tested against a number of other popular techniques and the obtained performance gains are reported using a number of synthetic fMRI data. Results with real data have also been obtained in the context of a number of experiments and will be soon reported in a different publication.