InfiniteWalk: Deep Network Embeddings as Laplacian Embeddings with a Nonlinearity
Paper and Code
May 29, 2020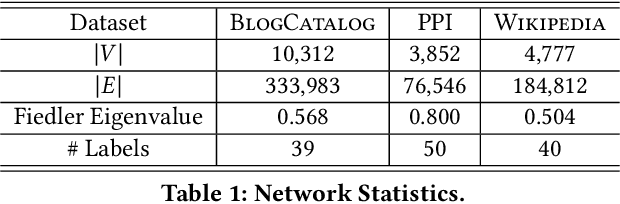
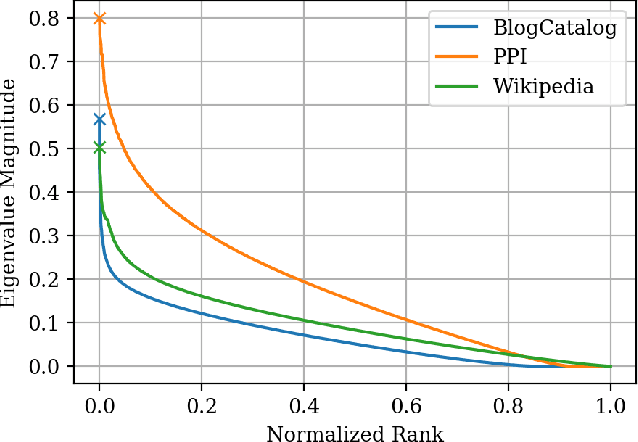

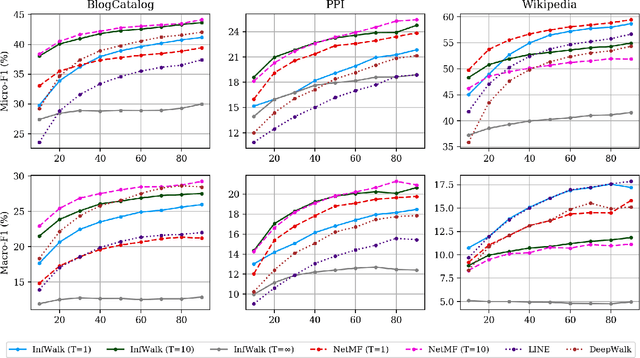
The skip-gram model for learning word embeddings (Mikolov et al. 2013) has been widely popular, and DeepWalk (Perozzi et al. 2014), among other methods, has extended the model to learning node representations from networks. Recent work of Qiu et al. (2018) provides a closed-form expression for the DeepWalk objective, obviating the need for sampling for small datasets and improving accuracy. In these methods, the "window size" T within which words or nodes are considered to co-occur is a key hyperparameter. We study the objective in the limit as T goes to infinity, which allows us to simplify the expression of Qiu et al. We prove that this limiting objective corresponds to factoring a simple transformation of the pseudoinverse of the graph Laplacian, linking DeepWalk to extensive prior work in spectral graph embeddings. Further, we show that by a applying a simple nonlinear entrywise transformation to this pseudoinverse, we recover a good approximation of the finite-T objective and embeddings that are competitive with those from DeepWalk and other skip-gram methods in multi-label classification. Surprisingly, we find that even simple binary thresholding of the Laplacian pseudoinverse is often competitive, suggesting that the core advancement of recent methods is a nonlinearity on top of the classical spectral embedding approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge