Index $t$-SNE: Tracking Dynamics of High-Dimensional Datasets with Coherent Embeddings
Paper and Code
Sep 22, 2021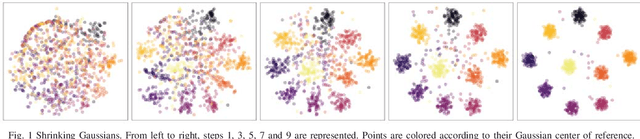


$t$-SNE is an embedding method that the data science community has widely Two interesting characteristics of t-SNE are the structure preservation property and the answer to the crowding problem, where all neighbors in high dimensional space cannot be represented correctly in low dimensional space. $t$-SNE preserves the local neighborhood, and similar items are nicely spaced by adjusting to the local density. These two characteristics produce a meaningful representation, where the cluster area is proportional to its size in number, and relationships between clusters are materialized by closeness on the embedding. This algorithm is non-parametric, therefore two initializations of the algorithm would lead to two different embedding. In a forensic approach, analysts would like to compare two or more datasets using their embedding. An approach would be to learn a parametric model over an embedding built with a subset of data. While this approach is highly scalable, points could be mapped at the same exact position, making them indistinguishable. This type of model would be unable to adapt to new outliers nor concept drift. This paper presents a methodology to reuse an embedding to create a new one, where cluster positions are preserved. The optimization process minimizes two costs, one relative to the embedding shape and the second relative to the support embedding' match. The proposed algorithm has the same complexity than the original $t$-SNE to embed new items, and a lower one when considering the embedding of a dataset sliced into sub-pieces. The method showed promising results on a real-world dataset, allowing to observe the birth, evolution and death of clusters. The proposed approach facilitates identifying significant trends and changes, which empowers the monitoring high dimensional datasets' dynamics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge