Incremental Learning Through Deep Adaptation
Paper and Code
Feb 13, 2018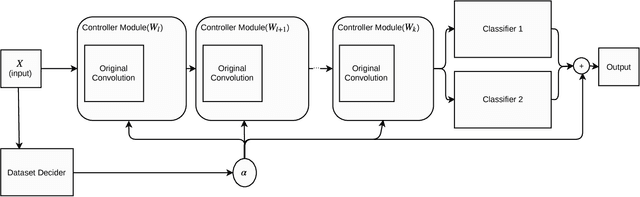

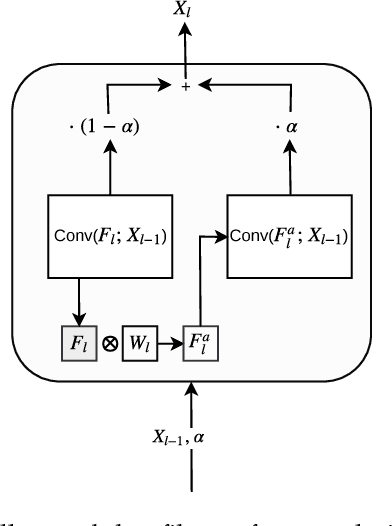
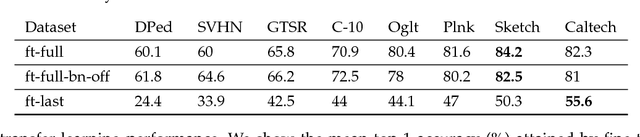
Given an existing trained neural network, it is often desirable to learn new capabilities without hindering performance of those already learned. Existing approaches either learn sub-optimal solutions, require joint training, or incur a substantial increment in the number of parameters for each added domain, typically as many as the original network. We propose a method called \emph{Deep Adaptation Networks} (DAN) that constrains newly learned filters to be linear combinations of existing ones. DANs precisely preserve performance on the original domain, require a fraction (typically 13\%, dependent on network architecture) of the number of parameters compared to standard fine-tuning procedures and converge in less cycles of training to a comparable or better level of performance. When coupled with standard network quantization techniques, we further reduce the parameter cost to around 3\% of the original with negligible or no loss in accuracy. The learned architecture can be controlled to switch between various learned representations, enabling a single network to solve a task from multiple different domains. We conduct extensive experiments showing the effectiveness of our method on a range of image classification tasks and explore different aspects of its behavior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge