Improving reproducibility in synchrotron tomography using implementation-adapted filters
Paper and Code
Mar 15, 2021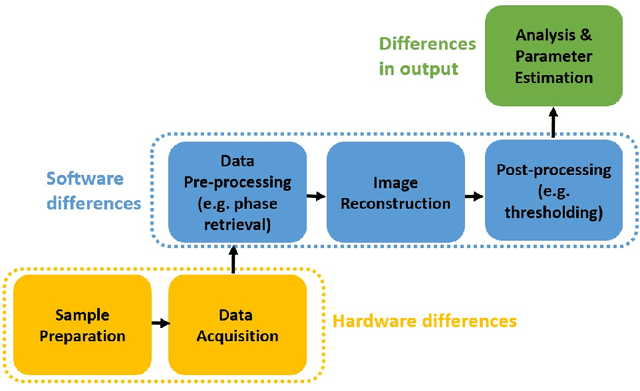

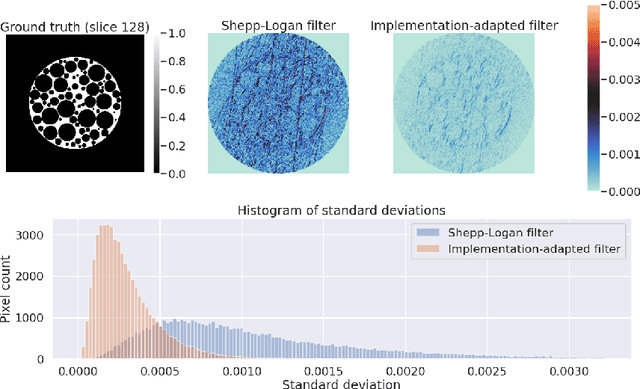

For reconstructing large tomographic datasets fast, filtered backprojection-type or Fourier-based algorithms are still the method of choice, as they have been for decades. These robust and computationally efficient algorithms have been integrated in a broad range of software packages. Despite the fact that the underlying mathematical formulas used for image reconstruction are unambiguous, variations in discretisation and interpolation result in quantitative differences between reconstructed images obtained from different software. This hinders reproducibility of experimental results. In this paper, we propose a way to reduce such differences by optimising the filter used in analytical algorithms. These filters can be computed using a wrapper routine around a black-box implementation of a reconstruction algorithm, and lead to quantitatively similar reconstructions. We demonstrate use cases for our approach by computing implementation-adapted filters for several open-source implementations and applying it to simulated phantoms and real-world data acquired at the synchrotron. Our contribution to a reproducible reconstruction step forms a building block towards a fully reproducible synchrotron tomography data processing pipeline.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge