Improved Bilinear Pooling with CNNs
Paper and Code
Jul 21, 2017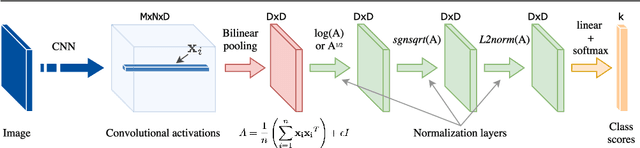
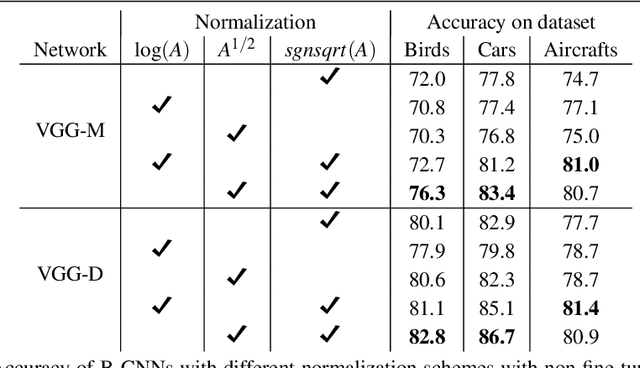
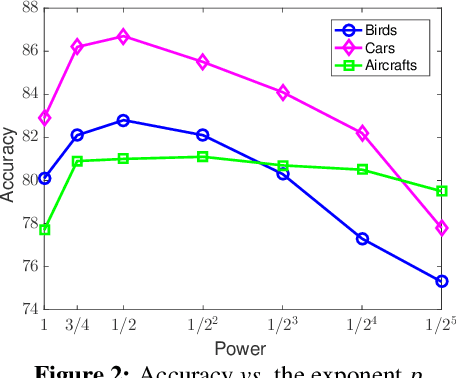

Bilinear pooling of Convolutional Neural Network (CNN) features [22, 23], and their compact variants [10], have been shown to be effective at fine-grained recognition, scene categorization, texture recognition, and visual question-answering tasks among others. The resulting representation captures second-order statistics of convolutional features in a translationally invariant manner. In this paper we investigate various ways of normalizing these statistics to improve their representation power. In particular we find that the matrix square-root normalization offers significant improvements and outperforms alternative schemes such as the matrix logarithm normalization when combined with elementwise square-root and l2 normalization. This improves the accuracy by 2-3% on a range of fine-grained recognition datasets leading to a new state of the art. We also investigate how the accuracy of matrix function computations effect network training and evaluation. In particular we compare against a technique for estimating matrix square-root gradients via solving a Lyapunov equation that is more numerically accurate than computing gradients via a Singular Value Decomposition (SVD). We find that while SVD gradients are numerically inaccurate the overall effect on the final accuracy is negligible once boundary cases are handled carefully. We present an alternative scheme for computing gradients that is faster and yet it offers improvements over the baseline model. Finally we show that the matrix square-root computed approximately using a few Newton iterations is just as accurate for the classification task but allows an order-of-magnitude faster GPU implementation compared to SVD decomposition.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge