Implicit Regularization in Tensor Factorization
Paper and Code
Feb 26, 2021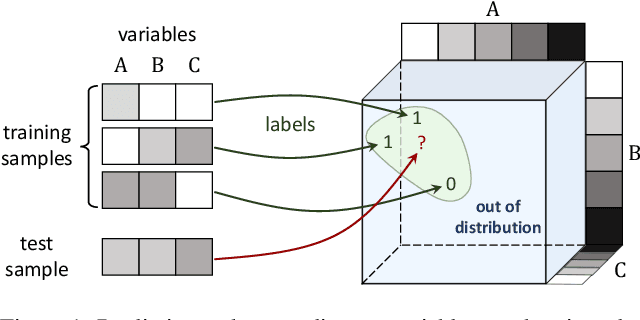

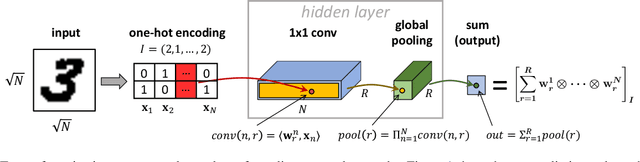

Implicit regularization in deep learning is perceived as a tendency of gradient-based optimization to fit training data with predictors of minimal "complexity." The fact that only some types of data give rise to generalization is understood to result from them being especially amenable to fitting with low complexity predictors. A major challenge in formalizing this intuition is to define complexity measures that are quantitative yet capture the essence of data that admits generalization. With an eye towards this challenge, we provide the first analysis of implicit regularization in tensor factorization, equivalent to a certain non-linear neural network. We characterize the dynamics that gradient descent induces on the factorization, and establish a bias towards low tensor rank, in compliance with empirical evidence. Then, motivated by tensor rank capturing implicit regularization of a non-linear neural network, we empirically explore it as a measure of complexity, and find that it stays extremely low when fitting standard datasets. This leads us to believe that tensor rank may pave way to explaining both implicit regularization of neural networks, and the properties of real-world data translating this implicit regularization to generalization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge