Implicit Gradient Regularization
Paper and Code
Sep 23, 2020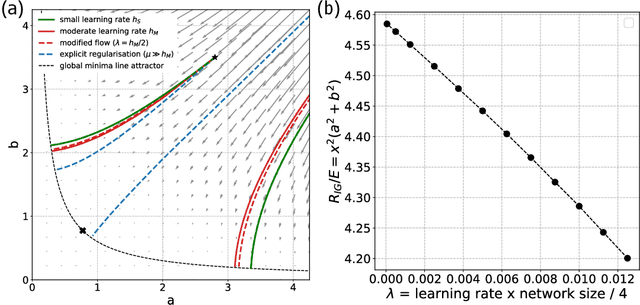
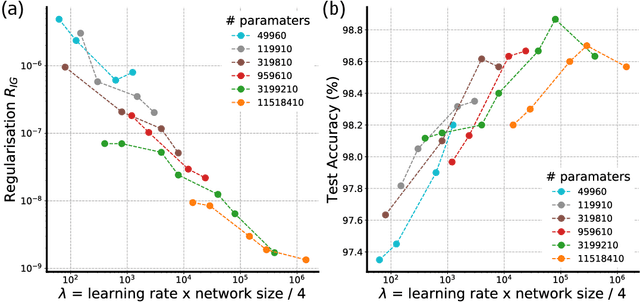
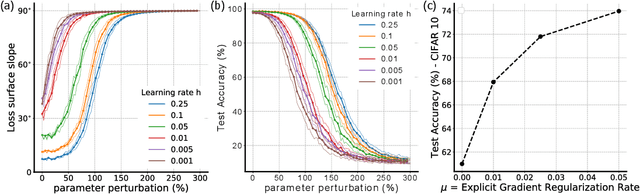

Gradient descent can be surprisingly good at optimizing deep neural networks without overfitting and without explicit regularization. We find that the discrete steps of gradient descent implicitly regularize models by penalizing gradient descent trajectories that have large loss gradients. We call this Implicit Gradient Regularization (IGR) and we use backward error analysis to calculate the size of this regularization. We confirm empirically that implicit gradient regularization biases gradient descent toward flat minima, where test errors are small and solutions are robust to noisy parameter perturbations. Furthermore, we demonstrate that the implicit gradient regularization term can be used as an explicit regularizer, allowing us to control this gradient regularization directly. More broadly, our work indicates that backward error analysis is a useful theoretical approach to the perennial question of how learning rate, model size, and parameter regularization interact to determine the properties of overparameterized models optimized with gradient descent.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge