Impedance Optimization for Uncertain Contact Interactions Through Risk Sensitive Optimal Control
Paper and Code
Nov 09, 2020


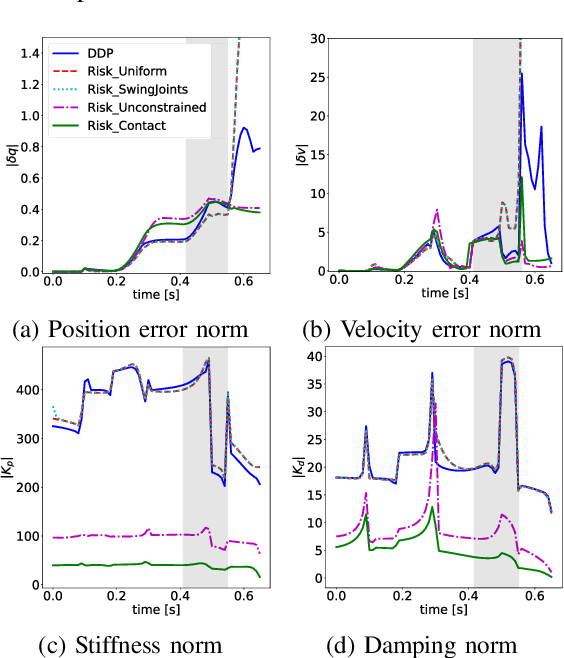
This paper addresses the problem of computing optimal impedance schedules for legged locomotion tasks involving complex contact interactions. We formulate the problem of impedance regulation as a trade-off between disturbance rejection and measurement uncertainty. We extend a stochastic optimal control algorithm known as Risk Sensitive Control to take into account measurement uncertainty and propose a formal way to include such uncertainty for unknown contact locations. The approach can efficiently generate optimal state and control trajectories along with local feedback control gains, i.e. impedance schedules. Extensive simulations demonstrate the capabilities of the approach in generating meaningful stiffness and damping modulation patterns before and after contact interaction. For example, contact forces are reduced during early contacts, damping increases to anticipate a high impact event and tracking is automatically traded-off for increased stability. In particular, we show a significant improvement in performance during jumping and trotting tasks with a simulated quadruped robot.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge