Image To Tree with Recursive Prompting
Paper and Code
Jan 01, 2023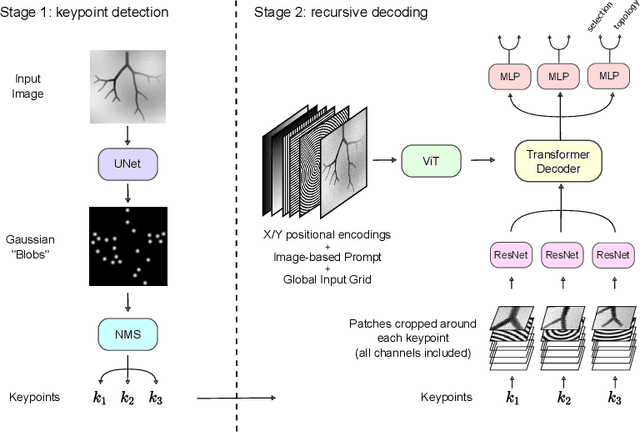
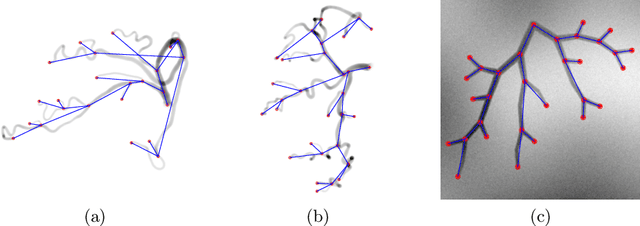

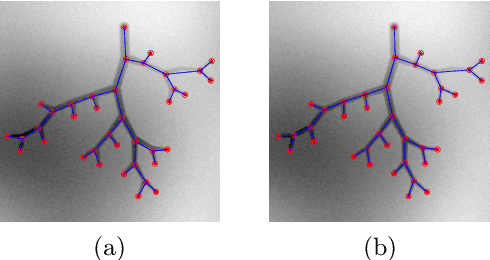
Extracting complex structures from grid-based data is a common key step in automated medical image analysis. The conventional solution to recovering tree-structured geometries typically involves computing the minimal cost path through intermediate representations derived from segmentation masks. However, this methodology has significant limitations in the context of projective imaging of tree-structured 3D anatomical data such as coronary arteries, since there are often overlapping branches in the 2D projection. In this work, we propose a novel approach to predicting tree connectivity structure which reformulates the task as an optimization problem over individual steps of a recursive process. We design and train a two-stage model which leverages the UNet and Transformer architectures and introduces an image-based prompting technique. Our proposed method achieves compelling results on a pair of synthetic datasets, and outperforms a shortest-path baseline.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge