Hypothesis Transfer Learning via Transformation Functions
Paper and Code
Nov 05, 2017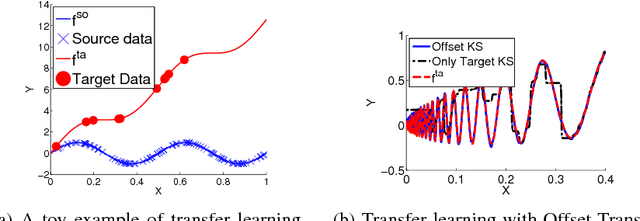
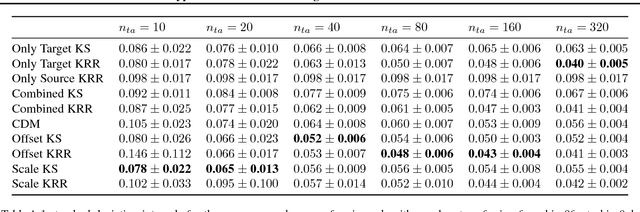
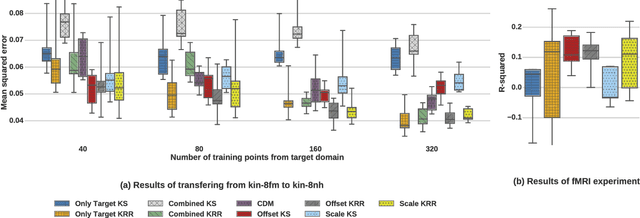
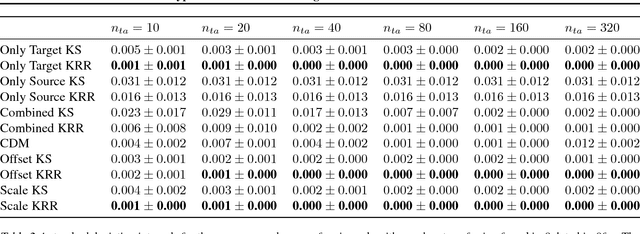
We consider the Hypothesis Transfer Learning (HTL) problem where one incorporates a hypothesis trained on the source domain into the learning procedure of the target domain. Existing theoretical analysis either only studies specific algorithms or only presents upper bounds on the generalization error but not on the excess risk. In this paper, we propose a unified algorithm-dependent framework for HTL through a novel notion of transformation function, which characterizes the relation between the source and the target domains. We conduct a general risk analysis of this framework and in particular, we show for the first time, if two domains are related, HTL enjoys faster convergence rates of excess risks for Kernel Smoothing and Kernel Ridge Regression than those of the classical non-transfer learning settings. Experiments on real world data demonstrate the effectiveness of our framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge