HyperVQ: MLR-based Vector Quantization in Hyperbolic Space

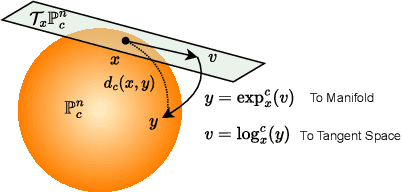
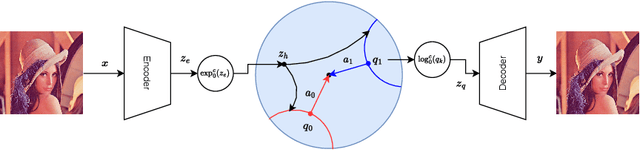
The success of models operating on tokenized data has led to an increased demand for effective tokenization methods, particularly when applied to vision or auditory tasks, which inherently involve non-discrete data. One of the most popular tokenization methods is Vector Quantization (VQ), a key component of several recent state-of-the-art methods across various domains. Typically, a VQ Variational Autoencoder (VQVAE) is trained to transform data to and from its tokenized representation. However, since the VQVAE is trained with a reconstruction objective, there is no constraint for the embeddings to be well disentangled, a crucial aspect for using them in discriminative tasks. Recently, several works have demonstrated the benefits of utilizing hyperbolic spaces for representation learning. Hyperbolic spaces induce compact latent representations due to their exponential volume growth and inherent ability to model hierarchical and structured data. In this work, we explore the use of hyperbolic spaces for vector quantization (HyperVQ), formulating the VQ operation as a hyperbolic Multinomial Logistic Regression (MLR) problem, in contrast to the Euclidean K-Means clustering used in VQVAE. Through extensive experiments, we demonstrate that hyperVQ performs comparably in reconstruction and generative tasks while outperforming VQ in discriminative tasks and learning a highly disentangled latent space.