HyperInvariances: Amortizing Invariance Learning
Paper and Code
Jul 17, 2022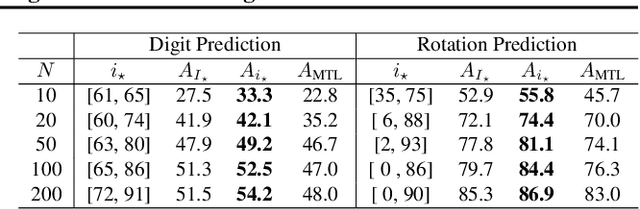
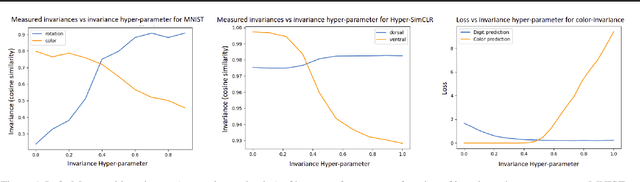

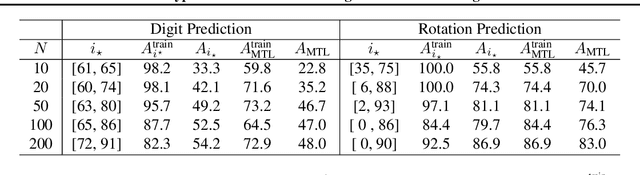
Providing invariances in a given learning task conveys a key inductive bias that can lead to sample-efficient learning and good generalisation, if correctly specified. However, the ideal invariances for many problems of interest are often not known, which has led both to a body of engineering lore as well as attempts to provide frameworks for invariance learning. However, invariance learning is expensive and data intensive for popular neural architectures. We introduce the notion of amortizing invariance learning. In an up-front learning phase, we learn a low-dimensional manifold of feature extractors spanning invariance to different transformations using a hyper-network. Then, for any problem of interest, both model and invariance learning are rapid and efficient by fitting a low-dimensional invariance descriptor an output head. Empirically, this framework can identify appropriate invariances in different downstream tasks and lead to comparable or better test performance than conventional approaches. Our HyperInvariance framework is also theoretically appealing as it enables generalisation-bounds that provide an interesting new operating point in the trade-off between model fit and complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge