How many samples are needed to leverage smoothness?

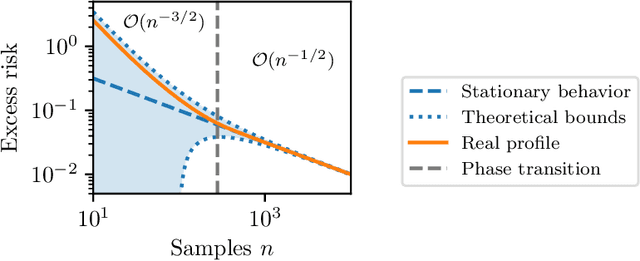
A core principle in statistical learning is that smoothness of target functions allows to break the curse of dimensionality. However, learning a smooth function through Taylor expansions requires enough samples close to one another to get meaningful estimate of high-order derivatives, which seems hard in machine learning problems where the ratio between number of data and input dimension is relatively small. Should we really hope to break the curse of dimensionality based on Taylor expansion estimation? What happens if Taylor expansions are replaced by Fourier or wavelet expansions? By deriving a new lower bound on the generalization error, this paper investigates the role of constants and transitory regimes which are usually not depicted beyond classical learning theory statements while that play a dominant role in practice.