How Many Pairwise Preferences Do We Need to Rank A Graph Consistently?
Paper and Code
Nov 06, 2018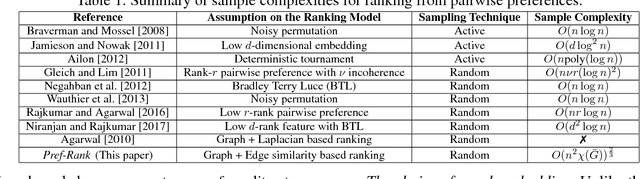
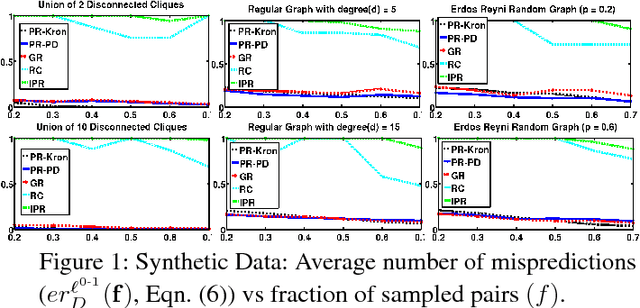
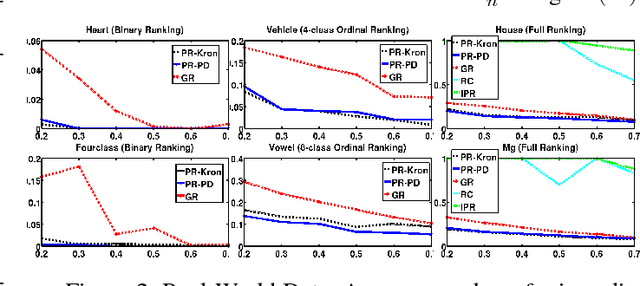

We consider the problem of optimal recovery of true ranking of $n$ items from a randomly chosen subset of their pairwise preferences. It is well known that without any further assumption, one requires a sample size of $\Omega(n^2)$ for the purpose. We analyze the problem with an additional structure of relational graph $G([n],E)$ over the $n$ items added with an assumption of \emph{locality}: Neighboring items are similar in their rankings. Noting the preferential nature of the data, we choose to embed not the graph, but, its \emph{strong product} to capture the pairwise node relationships. Furthermore, unlike existing literature that uses Laplacian embedding for graph based learning problems, we use a richer class of graph embeddings---\emph{orthonormal representations}---that includes (normalized) Laplacian as its special case. Our proposed algorithm, {\it Pref-Rank}, predicts the underlying ranking using an SVM based approach over the chosen embedding of the product graph, and is the first to provide \emph{statistical consistency} on two ranking losses: \emph{Kendall's tau} and \emph{Spearman's footrule}, with a required sample complexity of $O(n^2 \chi(\bar{G}))^{\frac{2}{3}}$ pairs, $\chi(\bar{G})$ being the \emph{chromatic number} of the complement graph $\bar{G}$. Clearly, our sample complexity is smaller for dense graphs, with $\chi(\bar G)$ characterizing the degree of node connectivity, which is also intuitive due to the locality assumption e.g. $O(n^\frac{4}{3})$ for union of $k$-cliques, or $O(n^\frac{5}{3})$ for random and power law graphs etc.---a quantity much smaller than the fundamental limit of $\Omega(n^2)$ for large $n$. This, for the first time, relates ranking complexity to structural properties of the graph. We also report experimental evaluations on different synthetic and real datasets, where our algorithm is shown to outperform the state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge