How Interpretable Are Interpretable Graph Neural Networks?
Paper and Code
Jun 12, 2024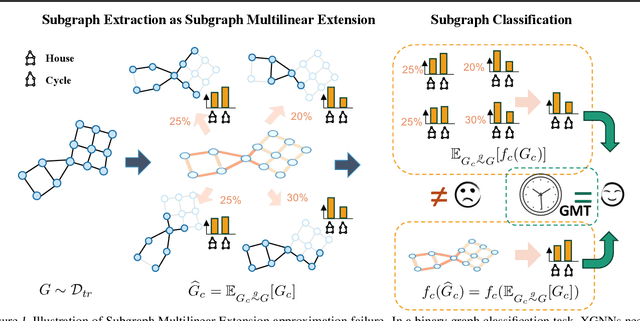
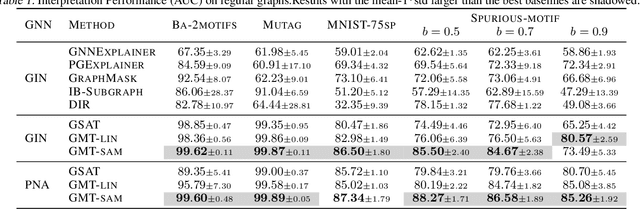
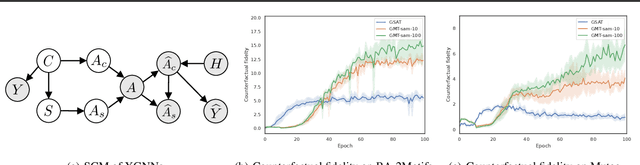
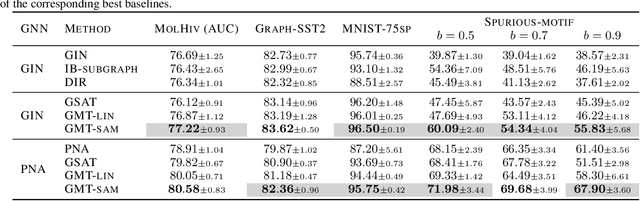
Interpretable graph neural networks (XGNNs ) are widely adopted in various scientific applications involving graph-structured data. Existing XGNNs predominantly adopt the attention-based mechanism to learn edge or node importance for extracting and making predictions with the interpretable subgraph. However, the representational properties and limitations of these methods remain inadequately explored. In this work, we present a theoretical framework that formulates interpretable subgraph learning with the multilinear extension of the subgraph distribution, coined as subgraph multilinear extension (SubMT). Extracting the desired interpretable subgraph requires an accurate approximation of SubMT, yet we find that the existing XGNNs can have a huge gap in fitting SubMT. Consequently, the SubMT approximation failure will lead to the degenerated interpretability of the extracted subgraphs. To mitigate the issue, we design a new XGNN architecture called Graph Multilinear neT (GMT), which is provably more powerful in approximating SubMT. We empirically validate our theoretical findings on a number of graph classification benchmarks. The results demonstrate that GMT outperforms the state-of-the-art up to 10% in terms of both interpretability and generalizability across 12 regular and geometric graph benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge