How Does the Smoothness Approximation Method Facilitate Generalization for Federated Adversarial Learning?
Paper and Code
Dec 11, 2024
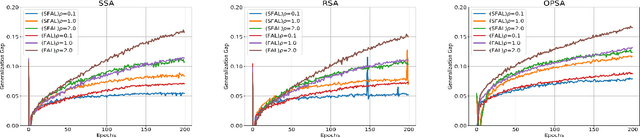
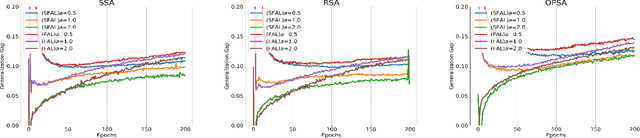
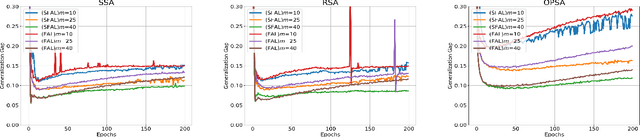
Federated Adversarial Learning (FAL) is a robust framework for resisting adversarial attacks on federated learning. Although some FAL studies have developed efficient algorithms, they primarily focus on convergence performance and overlook generalization. Generalization is crucial for evaluating algorithm performance on unseen data. However, generalization analysis is more challenging due to non-smooth adversarial loss functions. A common approach to addressing this issue is to leverage smoothness approximation. In this paper, we develop algorithm stability measures to evaluate the generalization performance of two popular FAL algorithms: \textit{Vanilla FAL (VFAL)} and {\it Slack FAL (SFAL)}, using three different smooth approximation methods: 1) \textit{Surrogate Smoothness Approximation (SSA)}, (2) \textit{Randomized Smoothness Approximation (RSA)}, and (3) \textit{Over-Parameterized Smoothness Approximation (OPSA)}. Based on our in-depth analysis, we answer the question of how to properly set the smoothness approximation method to mitigate generalization error in FAL. Moreover, we identify RSA as the most effective method for reducing generalization error. In highly data-heterogeneous scenarios, we also recommend employing SFAL to mitigate the deterioration of generalization performance caused by heterogeneity. Based on our theoretical results, we provide insights to help develop more efficient FAL algorithms, such as designing new metrics and dynamic aggregation rules to mitigate heterogeneity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge