How Does Data Diversity Shape the Weight Landscape of Neural Networks?
Paper and Code
Oct 18, 2024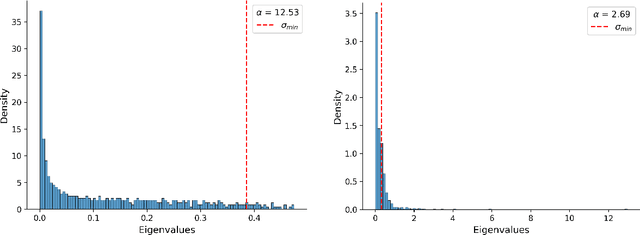
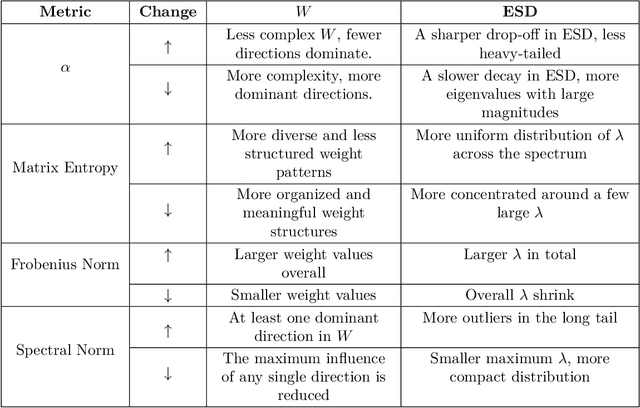
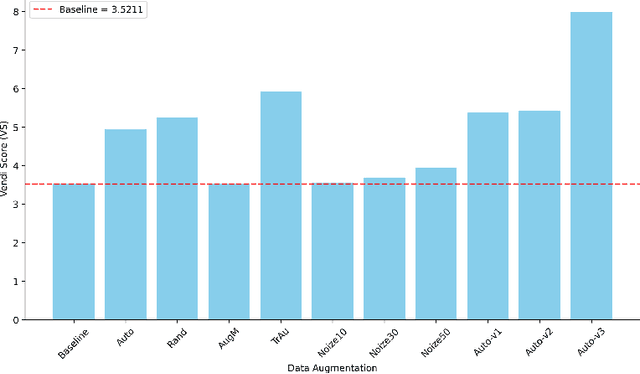
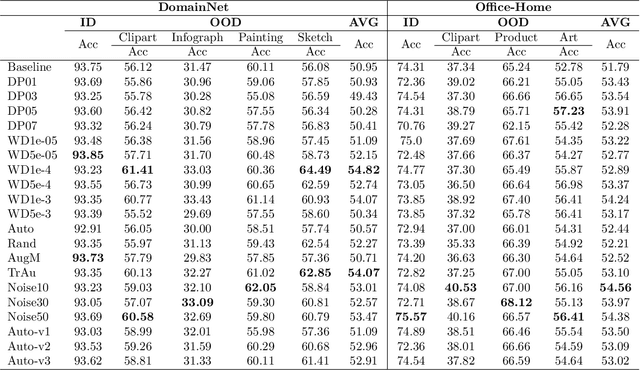
To enhance the generalization of machine learning models to unseen data, techniques such as dropout, weight decay ($L_2$ regularization), and noise augmentation are commonly employed. While regularization methods (i.e., dropout and weight decay) are geared toward adjusting model parameters to prevent overfitting, data augmentation increases the diversity of the input training set, a method purported to improve accuracy and calibration error. In this paper, we investigate the impact of each of these techniques on the parameter space of neural networks, with the goal of understanding how they alter the weight landscape in transfer learning scenarios. To accomplish this, we employ Random Matrix Theory to analyze the eigenvalue distributions of pre-trained models, fine-tuned using these techniques but using different levels of data diversity, for the same downstream tasks. We observe that diverse data influences the weight landscape in a similar fashion as dropout. Additionally, we compare commonly used data augmentation methods with synthetic data created by generative models. We conclude that synthetic data can bring more diversity into real input data, resulting in a better performance on out-of-distribution test instances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge