How Can Self-Attention Networks Recognize Dyck-n Languages?
Paper and Code
Oct 09, 2020
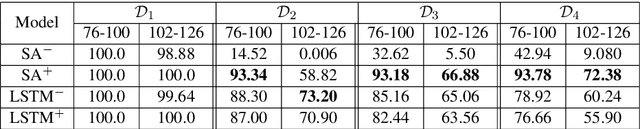
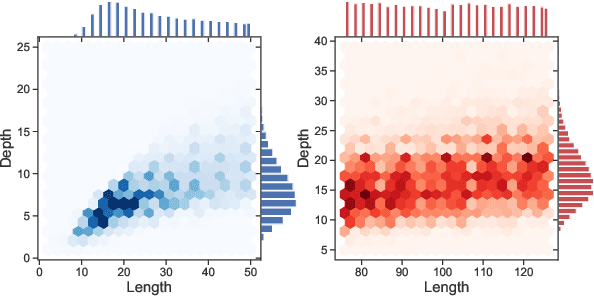
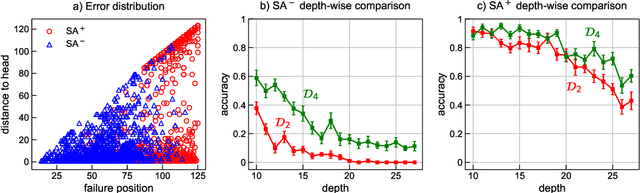
We focus on the recognition of Dyck-n ($\mathcal{D}_n$) languages with self-attention (SA) networks, which has been deemed to be a difficult task for these networks. We compare the performance of two variants of SA, one with a starting symbol (SA$^+$) and one without (SA$^-$). Our results show that SA$^+$ is able to generalize to longer sequences and deeper dependencies. For $\mathcal{D}_2$, we find that SA$^-$ completely breaks down on long sequences whereas the accuracy of SA$^+$ is 58.82$\%$. We find attention maps learned by $\text{SA}{^+}$ to be amenable to interpretation and compatible with a stack-based language recognizer. Surprisingly, the performance of SA networks is at par with LSTMs, which provides evidence on the ability of SA to learn hierarchies without recursion.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge