Householder-Absolute Neural Layers For High Variability and Deep Trainability
Paper and Code
Jun 08, 2021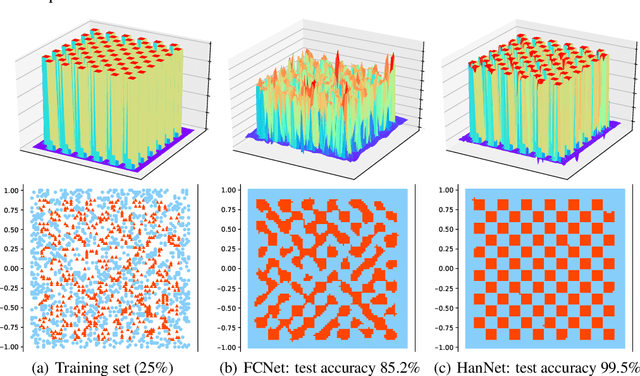
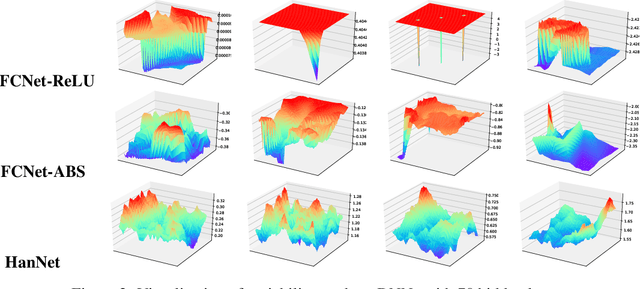

We propose a new architecture for artificial neural networks called Householder-absolute neural layers, or Han-layers for short, that use Householder reflectors as weight matrices and the absolute-value function for activation. Han-layers, functioning as fully connected layers, are motivated by recent results on neural-network variability and are designed to increase activation ratio and reduce the chance of Collapse to Constants. Neural networks constructed chiefly from Han-layers are called HanNets. By construction, HanNets enjoy a theoretical guarantee that vanishing or exploding gradient never occurs. We conduct several proof-of-concept experiments. Some surprising results obtained on styled test problems suggest that, under certain conditions, HanNets exhibit an unusual ability to produce nearly perfect solutions unattainable by fully connected networks. Experiments on regression datasets show that HanNets can significantly reduce the number of model parameters while maintaining or improving the level of generalization accuracy. In addition, by adding a few Han-layers into the pre-classification FC-layer of a convolutional neural network, we are able to quickly improve a state-of-the-art result on CIFAR10 dataset. These proof-of-concept results are sufficient to necessitate further studies on HanNets to understand their capacities and limits, and to exploit their potentials in real-world applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge