History-Restricted Online Learning
Paper and Code
May 28, 2022
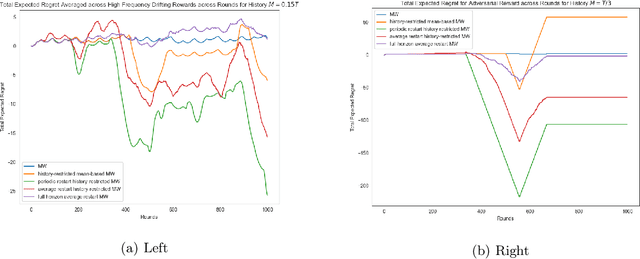
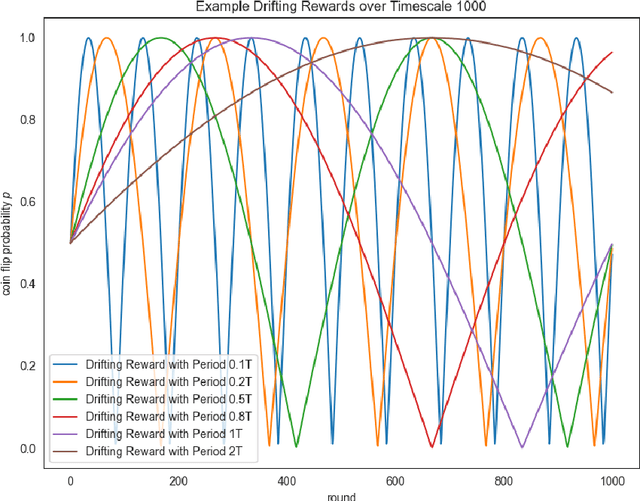
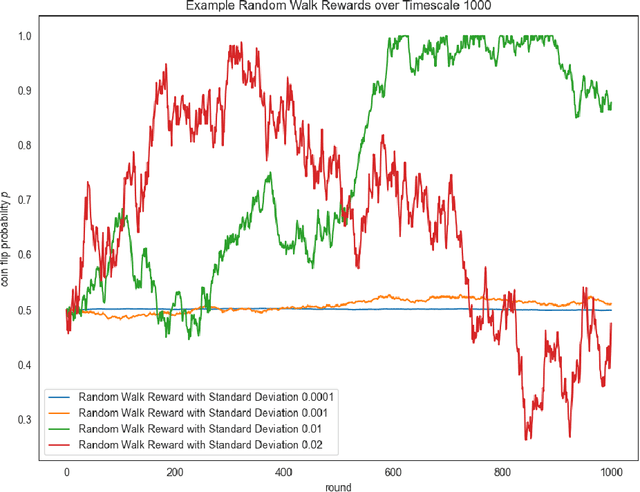
We introduce the concept of history-restricted no-regret online learning algorithms. An online learning algorithm $\mathcal{A}$ is $M$-history-restricted if its output at time $t$ can be written as a function of the $M$ previous rewards. This class of online learning algorithms is quite natural to consider from many perspectives: they may be better models of human agents and they do not store long-term information (thereby ensuring ``the right to be forgotten''). We first demonstrate that a natural approach to constructing history-restricted algorithms from mean-based no-regret learning algorithms (e.g. running Hedge over the last $M$ rounds) fails, and that such algorithms incur linear regret. We then construct a history-restricted algorithm that achieves a per-round regret of $\Theta(1/\sqrt{M})$, which we complement with a tight lower bound. Finally, we empirically explore distributions where history-restricted online learners have favorable performance compared to other no-regret algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge