High dimensional thresholded regression and shrinkage effect
Paper and Code
May 11, 2016


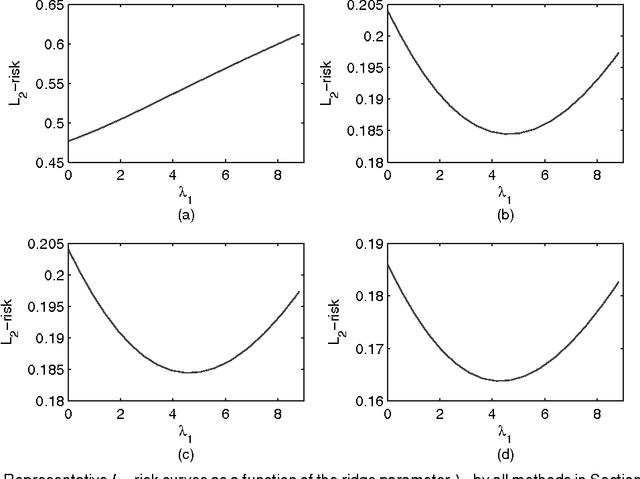
High-dimensional sparse modeling via regularization provides a powerful tool for analyzing large-scale data sets and obtaining meaningful, interpretable models. The use of nonconvex penalty functions shows advantage in selecting important features in high dimensions, but the global optimality of such methods still demands more understanding. In this paper, we consider sparse regression with hard-thresholding penalty, which we show to give rise to thresholded regression. This approach is motivated by its close connection with the $L_0$-regularization, which can be unrealistic to implement in practice but of appealing sampling properties, and its computational advantage. Under some mild regularity conditions allowing possibly exponentially growing dimensionality, we establish the oracle inequalities of the resulting regularized estimator, as the global minimizer, under various prediction and variable selection losses, as well as the oracle risk inequalities of the hard-thresholded estimator followed by a further $L_2$-regularization. The risk properties exhibit interesting shrinkage effects under both estimation and prediction losses. We identify the optimal choice of the ridge parameter, which is shown to have simultaneous advantages to both the $L_2$-loss and prediction loss. These new results and phenomena are evidenced by simulation and real data examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge