High-Dimensional Optimization in Adaptive Random Subspaces
Paper and Code
Jul 08, 2019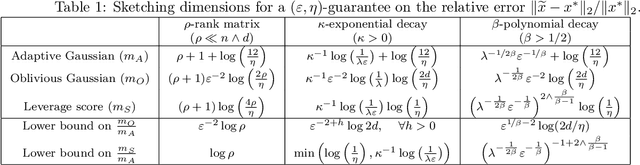

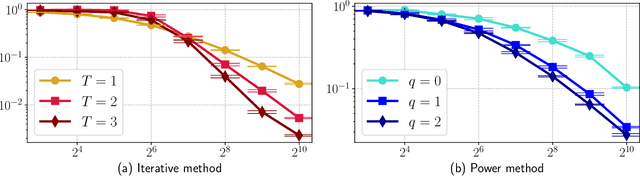

We propose a new randomized optimization method for high-dimensional problems which can be seen as a generalization of coordinate descent to random subspaces. We show that an adaptive sampling strategy for the random subspace significantly outperforms the oblivious sampling method, which is the common choice in the recent literature. The adaptive subspace can be efficiently generated by a correlated random matrix ensemble whose statistics mimic the input data. We prove that the improvement in the relative error of the solution can be tightly characterized in terms of the spectrum of the data matrix, and provide probabilistic upper-bounds. We then illustrate the consequences of our theory with data matrices of different spectral decay. Extensive experimental results show that the proposed approach offers significant speed ups in machine learning problems including logistic regression, kernel classification with random convolution layers and shallow neural networks with rectified linear units. Our analysis is based on convex analysis and Fenchel duality, and establishes connections to sketching and randomized matrix decomposition.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge