High-Dimensional Dependency Structure Learning for Physical Processes

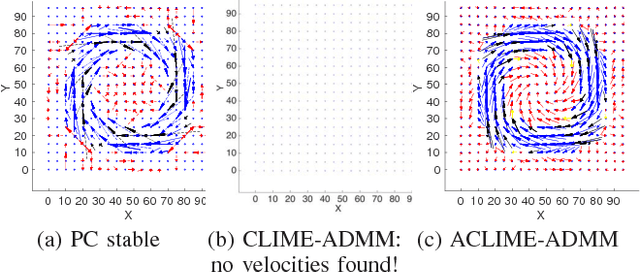
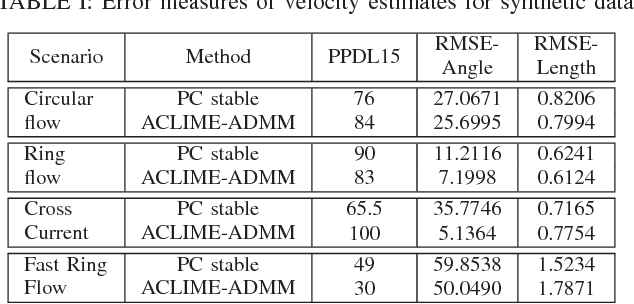
In this paper, we consider the use of structure learning methods for probabilistic graphical models to identify statistical dependencies in high-dimensional physical processes. Such processes are often synthetically characterized using PDEs (partial differential equations) and are observed in a variety of natural phenomena, including geoscience data capturing atmospheric and hydrological phenomena. Classical structure learning approaches such as the PC algorithm and variants are challenging to apply due to their high computational and sample requirements. Modern approaches, often based on sparse regression and variants, do come with finite sample guarantees, but are usually highly sensitive to the choice of hyper-parameters, e.g., parameter $\lambda$ for sparsity inducing constraint or regularization. In this paper, we present ACLIME-ADMM, an efficient two-step algorithm for adaptive structure learning, which estimates an edge specific parameter $\lambda_{ij}$ in the first step, and uses these parameters to learn the structure in the second step. Both steps of our algorithm use (inexact) ADMM to solve suitable linear programs, and all iterations can be done in closed form in an efficient block parallel manner. We compare ACLIME-ADMM with baselines on both synthetic data simulated by partial differential equations (PDEs) that model advection-diffusion processes, and real data (50 years) of daily global geopotential heights to study information flow in the atmosphere. ACLIME-ADMM is shown to be efficient, stable, and competitive, usually better than the baselines especially on difficult problems. On real data, ACLIME-ADMM recovers the underlying structure of global atmospheric circulation, including switches in wind directions at the equator and tropics entirely from the data.