High-Dimensional Data Set Simplification by Laplace-Beltrami Operator
Paper and Code
Mar 23, 2020
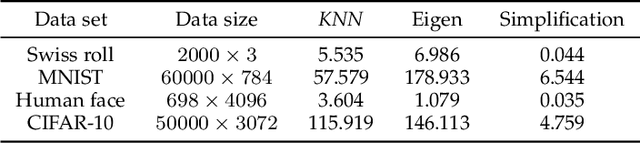

With the development of the Internet and other digital technologies, the speed of data generation has become considerably faster than the speed of data processing. Because big data typically contain massive redundant information, it is possible to significantly simplify a big data set while maintaining the key information it contains. In this paper, we develop a big data simplification method based on the eigenvalues and eigenfunctions of the Laplace-Beltrami operator (LBO). Specifically, given a data set that can be considered as an unorganized data point set in high-dimensional space, a discrete LBO defined on the big data set is constructed and its eigenvalues and eigenvectors are calculated. Then, the local extremum and the saddle points of the eigenfunctions are proposed to be the feature points of a data set in high-dimensional space, constituting a simplified data set. Moreover, we develop feature point detection methods for the functions defined on an unorganized data point set in high-dimensional space, and devise metrics for measuring the fidelity of the simplified data set to the original set. Finally, examples and applications are demonstrated to validate the efficiency and effectiveness of the proposed methods, demonstrating that data set simplification is a method for processing a maximum-sized data set using a limited data processing capability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge