Hierarchically Regularized Deep Forecasting

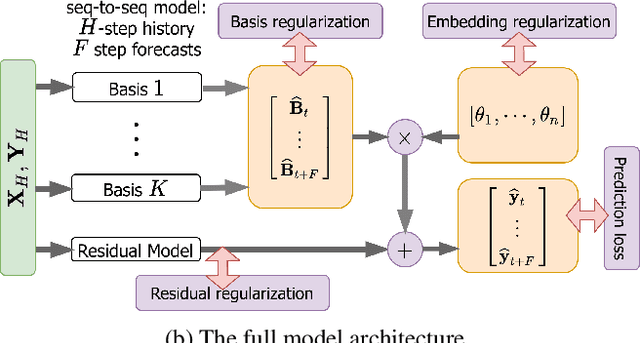
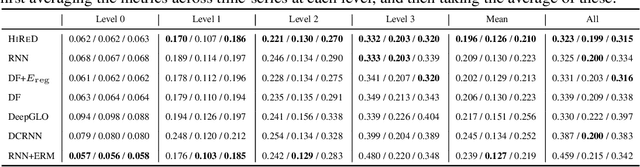
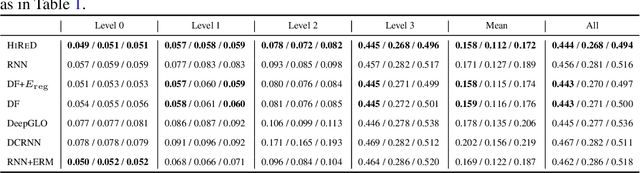
Hierarchical forecasting is a key problem in many practical multivariate forecasting applications - the goal is to simultaneously predict a large number of correlated time series that are arranged in a pre-specified aggregation hierarchy. The challenge is to exploit the hierarchical correlations to simultaneously obtain good prediction accuracy for time series at different levels of the hierarchy. In this paper, we propose a new approach for hierarchical forecasting based on decomposing the time series along a global set of basis time series and modeling hierarchical constraints using the coefficients of the basis decomposition for each time series. Unlike past methods, our approach is scalable at inference-time (forecasting for a specific time series only needs access to its own data) while (approximately) preserving coherence among the time series forecasts. We experiment on several publicly available datasets and demonstrate significantly improved overall performance on forecasts at different levels of the hierarchy, compared to existing state-of-the-art hierarchical reconciliation methods.