HEX: Hierarchical Emergence Exploitation in Self-Supervised Algorithms
Paper and Code
Oct 30, 2024
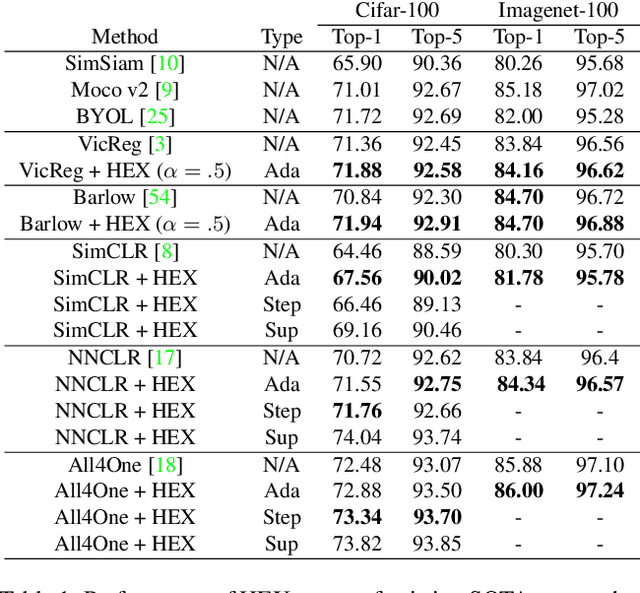

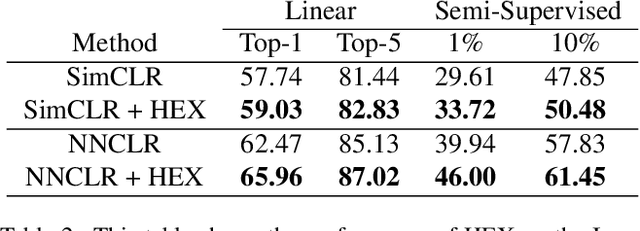
In this paper, we propose an algorithm that can be used on top of a wide variety of self-supervised (SSL) approaches to take advantage of hierarchical structures that emerge during training. SSL approaches typically work through some invariance term to ensure consistency between similar samples and a regularization term to prevent global dimensional collapse. Dimensional collapse refers to data representations spanning a lower-dimensional subspace. Recent work has demonstrated that the representation space of these algorithms gradually reflects a semantic hierarchical structure as training progresses. Data samples of the same hierarchical grouping tend to exhibit greater dimensional collapse locally compared to the dataset as a whole due to sharing features in common with each other. Ideally, SSL algorithms would take advantage of this hierarchical emergence to have an additional regularization term to account for this local dimensional collapse effect. However, the construction of existing SSL algorithms does not account for this property. To address this, we propose an adaptive algorithm that performs a weighted decomposition of the denominator of the InfoNCE loss into two terms: local hierarchical and global collapse regularization respectively. This decomposition is based on an adaptive threshold that gradually lowers to reflect the emerging hierarchical structure of the representation space throughout training. It is based on an analysis of the cosine similarity distribution of samples in a batch. We demonstrate that this hierarchical emergence exploitation (HEX) approach can be integrated across a wide variety of SSL algorithms. Empirically, we show performance improvements of up to 5.6% relative improvement over baseline SSL approaches on classification accuracy on Imagenet with 100 epochs of training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge