Heterogeneity for the Win: One-Shot Federated Clustering
Paper and Code
Mar 01, 2021
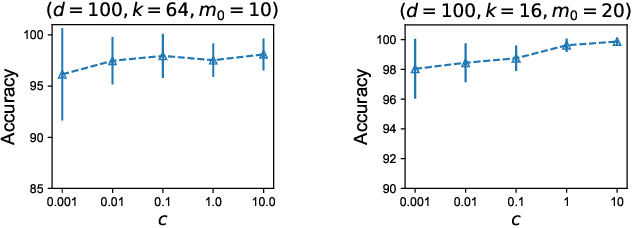
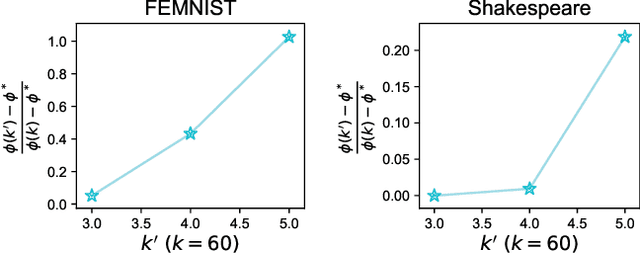
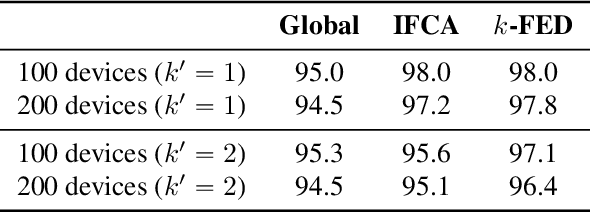
In this work, we explore the unique challenges -- and opportunities -- of unsupervised federated learning (FL). We develop and analyze a one-shot federated clustering scheme, $k$-FED, based on the widely-used Lloyd's method for $k$-means clustering. In contrast to many supervised problems, we show that the issue of statistical heterogeneity in federated networks can in fact benefit our analysis. We analyse $k$-FED under a center separation assumption and compare it to the best known requirements of its centralized counterpart. Our analysis shows that in heterogeneous regimes where the number of clusters per device $(k')$ is smaller than the total number of clusters over the network $k$, $(k'\le \sqrt{k})$, we can use heterogeneity to our advantage -- significantly weakening the cluster separation requirements for $k$-FED. From a practical viewpoint, $k$-FED also has many desirable properties: it requires only round of communication, can run asynchronously, and can handle partial participation or node/network failures. We motivate our analysis with experiments on common FL benchmarks, and highlight the practical utility of one-shot clustering through use-cases in personalized FL and device sampling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge