Hedging the Drift: Learning to Optimize under Non-Stationarity

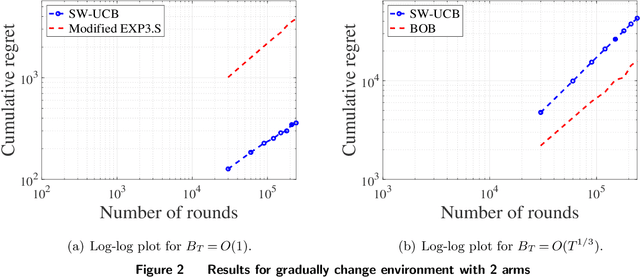
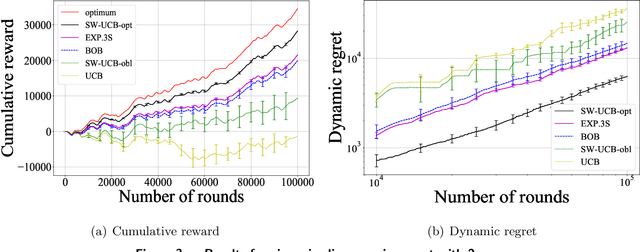
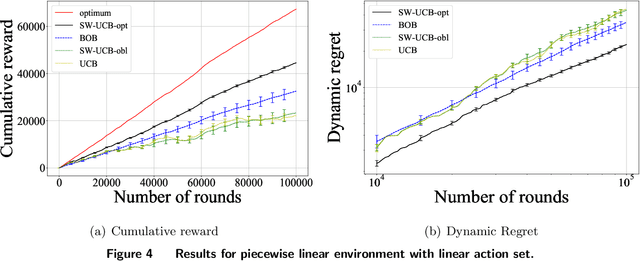
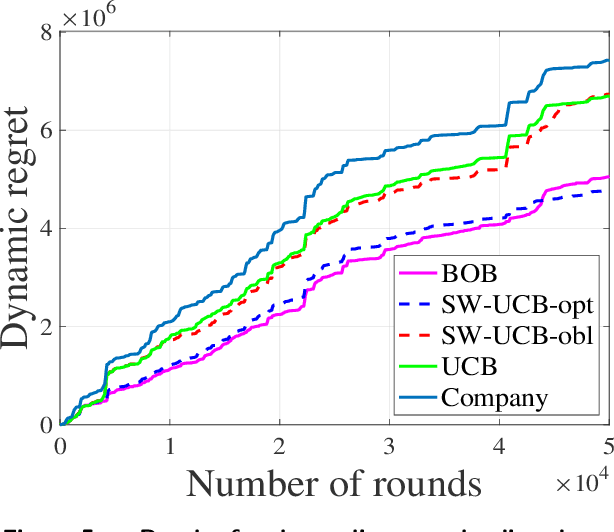
We introduce general data-driven decision-making algorithms that achieve state-of-the-art \emph{dynamic regret} bounds for non-stationary bandit settings. It captures applications such as advertisement allocation and dynamic pricing in changing environments. We show how the difficulty posed by the (unknown \emph{a priori} and possibly adversarial) non-stationarity can be overcome by an unconventional marriage between stochastic and adversarial bandit learning algorithms. Our main contribution is a general algorithmic recipe that first converts the rate-optimal Upper-Confidence-Bound (UCB) algorithm for stationary bandit settings into a tuned Sliding Window-UCB algorithm with optimal dynamic regret for the corresponding non-stationary counterpart. Boosted by the novel bandit-over-bandit framework with automatic adaptation to the unknown changing environment, it even permits us to enjoy, in a (surprisingly) parameter-free manner, this optimal dynamic regret if the amount of non-stationarity is moderate to large or an improved (compared to existing literature) dynamic regret otherwise. In addition to the classical exploration-exploitation trade-off, our algorithms leverage the power of the "forgetting principle" in their online learning processes, which is vital in changing environments. We further conduct extensive numerical experiments on both synthetic data and the CPRM-12-001: On-Line Auto Lending dataset provided by the Center for Pricing and Revenue Management at Columbia University to show that our proposed algorithms achieve superior dynamic regret performances.