Hcore-Init: Neural Network Initialization based on Graph Degeneracy
Paper and Code
Apr 16, 2020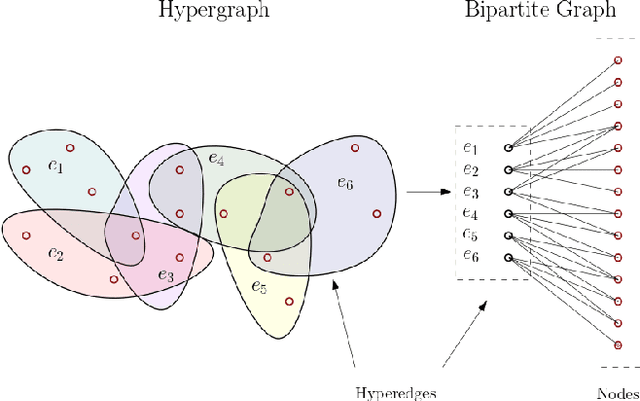

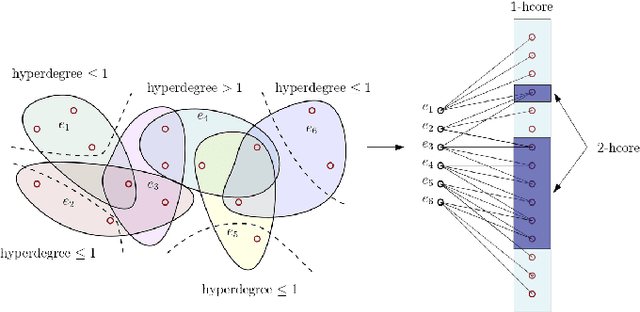
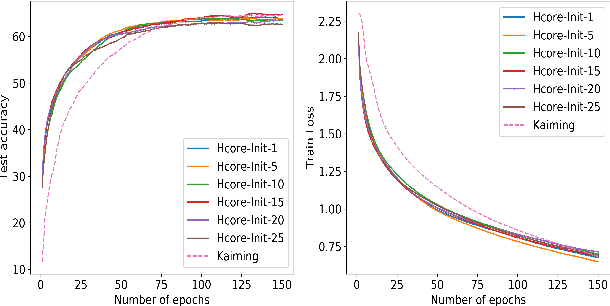
Neural networks are the pinnacle of Artificial Intelligence, as in recent years we witnessed many novel architectures, learning and optimization techniques for deep learning. Capitalizing on the fact that neural networks inherently constitute multipartite graphs among neuron layers, we aim to analyze directly their structure to extract meaningful information that can improve the learning process. To our knowledge graph mining techniques for enhancing learning in neural networks have not been thoroughly investigated. In this paper we propose an adapted version of the k-core structure for the complete weighted multipartite graph extracted from a deep learning architecture. As a multipartite graph is a combination of bipartite graphs, that are in turn the incidence graphs of hypergraphs, we design k-hypercore decomposition, the hypergraph analogue of k-core degeneracy. We applied k-hypercore to several neural network architectures, more specifically to convolutional neural networks and multilayer perceptrons for image recognition tasks after a very short pretraining. Then we used the information provided by the hypercore numbers of the neurons to re-initialize the weights of the neural network, thus biasing the gradient optimization scheme. Extensive experiments proved that k-hypercore outperforms the state-of-the-art initialization methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge